Hi @quantumdeveloper I find this simple method based on integral calculation.
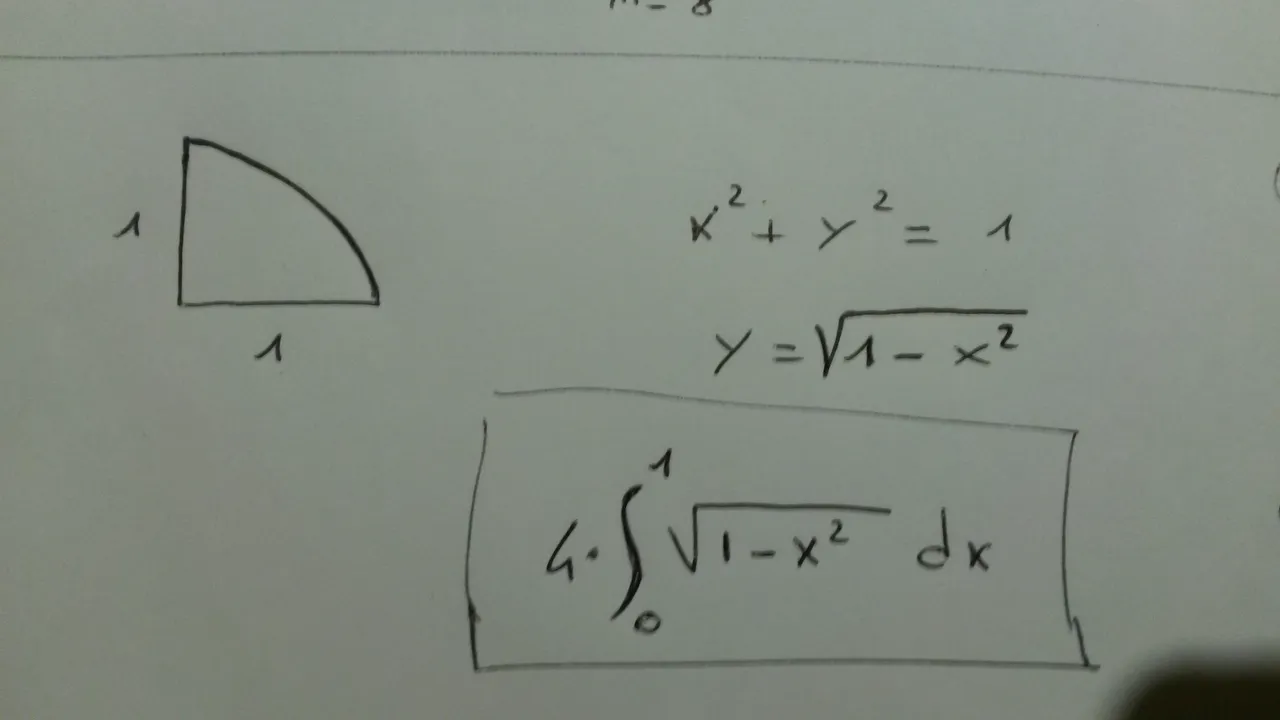
We know that the area of a circle is exactly π if the radius is 1.
And the equation of this circumference is: x^2 + y^2 = 1
So for x positive (x from 0 to 1) : y = sqrt(1-x^2)
I considered a quarter of circumference and calculate its area with an integral, then multiplied the result by 4.
I made a short script on Python, here is it the code (calcola means calculate)

The variable n represents the number of intervals in which I divided the x asses from 0 to 1.
And here it is the calculation
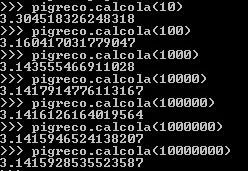
So with 10 milions of intervals I found π correct up to the sixth digit....not enough!!
This method is very slow...I don't recommend it for large calculation
If I find time I will try with another method. A geometrical one!
Bye bye
RE: Computation Contest #7 [2 SBI]