 By geralt on pixabay.com
By geralt on pixabay.com
As some of you know, I recently finished my B.Sc. in biology. As fewer of you know, I will start my Master's not this, but next year. This leaves me some time for other things (like working part-time in a biopharmaceutical lab, being the COO of Utopian, you know, mundane stuff).
For my biopharmaceutical lab job, I needed to be enrolled as a student, because else they'd have to pay me more, and thus not hire me. Capitalism in action.
This left me with the question what I should enroll in. Of course, I wouldn't need to actually pass the class, but the thought of not accomplishing anything useful frustrated me, which led to the decision of enrolling as a computer science student and taking programming classes.
Now, the classes use SML, a functional programming language that I won't really use in my life.
But
SML is a good basis to get a general understanding for how programming works. It's very mathematical and will (hopefully) teach me how to think in code.
And because nothing is really accomplished if it hasn't been told to anyone, I've decided to share some of the things I'm doing for those classes. On this blog, because I don't think it's high quality enough for my main blog.
Still, I'll write this with the assumption that those reading it can't code, because why would you want to read this otherwise?
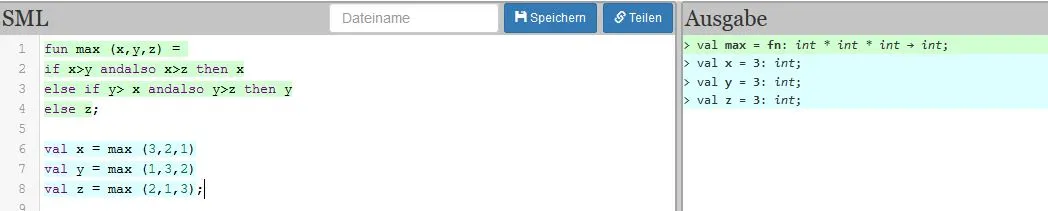
- Task 1: Write a function that gives you the highest of three numbers. Use conditionals.
A "conditional" is the "if - then - else" construct, and one of the things that are easiest to understand (in my opinion), because it's basically "normal" language. But be careful, in case you're dating a programmer because the conditional might get you some unwanted results.
"Go to the supermarket. If they have eggs then bring 10 else try another supermarket." Will get you the 10 eggs.
"Go to the supermarket. Buy milk, if they have eggs then bring 10, else try another supermarket." Will get you 10 cartons of milk, if the supermarket had eggs.
For my "give me the highest number" function, I chose x,y,z as variables, then checked if x is bigger than both y and z. If it was not, I compared y and z to see which of those is higher. Easy.
- Task 2: Calculate the cross sum of a number, once using a recursion and once using a tail recursion."
What's a recursion? Basically, you calculate something, take the result, put it in your original statement, and do the whole process all over again, until you reach a specific result.
A tail recursion is similar, but you don't have to "remember" the result you got before, which uses up fewer resources.

What I did here first is the recursion. x div 10 means I divide x by 10, and all I get is the number with the decimals shaved off. For example, 21 div 10 would give me a 2.
x mod 10 is similar, just the other way around: It gives me what's left after the divison. 21 mod 10 would give me 1.
So, quer (for "Quersumme", which is German for "cross sum") first checks if x div 10 is smaller than 1 (which would be the case for all (positive) numbers between 1 and 9). If that's the case, it gives back exactly this number.
If not, the function uses itself again, but changes x to x div 10 (example: 12 becomes 1) and adds x mod 10 (in this example, creating the formula quer (1) + 2).
Then it starts over. Now, 1 div 10 is smaller than 1, so we keep the 1. We now have 1+2. The result? 3. We successfully calculated the cross sum!
The tail recursion quer2 does something similar, with one small difference: We don't add a + something to the function, which allows us to throw everything that happened before out.
In the first step, it again tests if x mod 10 is smaller than 1 and gives out xif that's the case. So far, so good.
But if x mod 10isn't smaller than 1, the"help function" quer'comes into play.
What does quer' do? In contrary to querand quer2it has two variables, xand y.
If you take a peek at the examples that come after, you'll see that I set the value of y to 0.
Now, let's take an x for which x div 10 >= 1 and see what quer' does with that.
quer'(12,0)
12 mod 10 < 1 ?
-> 12 mod 10 = 2, false!
-> change quer'(12,0) to quer'(12 div 10, 0 + 12 mod 10)
(repeat from the beginning with new values)
quer'(1,2)
-> 1 mod 10 < 1 ?
-> 1 mod 10 = 1, false!
-> change quer'(1,2) to quer'(1 div 10, 2 + 1 mod 10)
(repeat from the beginning with new values)
quer'(0,3)
-> 0 mod 10 < 1?
-> 0 mod 10 = 0, true!
-> 3 + 0 mod 10
-> 3
Aaaaand we have our result!
There's a couple more exercises I already did, but I think I should split it up in more posts, as it might get a bit overloaded.
Feel free to ask questions in the comments.