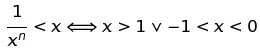Solution
The problem of this contest was to proof an equivalence:
I also just noticed that this inequation only holds for uneven, positive values of n(which is probably the reason why I had no entries this week).
First of all a small explanation why this is even true:
if x is bigger than 0: Then 1/x^n is only < 1 if x > 1.
if x is smaller 0: Then 1/x^n is only < -1 if x > -1
These two cases connect both inequations.
In this case you can rearrange the leftern inequation to:
1 < x^(n+1) if x > 0 → x > 1
1 > x^(n+1) if x < 0 → 1 > ±x → -1 < ±x → -1 < x
The ± comes from taking an even root.
So if x > 0 than x > 1 is the only solution and if x < 0, x > -1 is the only solution.
Putting the 2 together gets the rightern side of the equivalence:
x > 1 or -1 < x < 0
And the way back to prove it actually is an equivalence:
x > 1 → x^(n+1) > 1 → x > 1/x^n
-1 < x < 0 → 1 < x^(n+1) → x > 1/x^n
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
List of participants with their entries:
| Name | solution found | comment |
|---|---|---|
| @tonimontana | none | found one of the errors I made → you get the reward |
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Winner draw:
Not necessary since only 1 participant:
Congratulations @tonimontana , you won 2 SBI!
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓