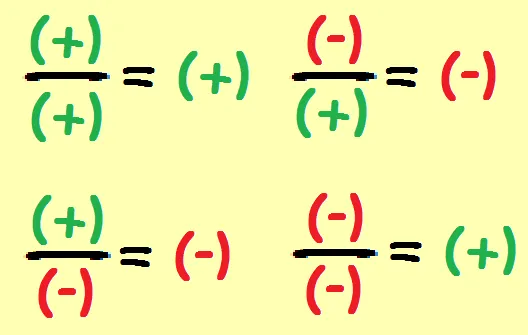
Suma de números enteros
Al sumar números enteros nos podemos encontrar con dos casos: Suma de números enteros con igual signo o también suma de números enteros con signos diferentes. En cada caso, debemos seguir una práctica regla que nos llevará a realizar tales operaciones de manera correcta. A continuación, les describo cada caso:


(+7) + (+13) = +20 , es como si estuviesen sumando haberes, es decir, tienes 7 por un lado y 13 por otro, entonces tienes 20.
(-3) + (- 11) = -14, acá es como si sumaras deudas, le debes 3 a una persona y sumas otra deuda de 11, entonces “debes” 14 (por eso lo negativo).


(-3) + (+ 12) = +9 , acá es como si tienes una “deuda” de 3 (lo negativo) pero “tienes” 12, algo así, como que pagas con lo que tienes pero sigues teniendo 9 ( como sigues "teniendo", por ello es positivo)
(+5) + (-15) = -10, acá tómalo como que tienes 5 pero debes 15, al final restas de lo que debes 5 que tienes , para bajar tu deuda, pero continúas debiendo 10.
Restra o sustracción en Z
La resta de números enteros se debe realizar tal como se indica a continuación:


4 – 9 = 4 + ( -9) = -5 , luego podemos asumir que toda resta es una suma lo que sucede es que sumamos el opuesto del sustraendo
Multiplicación en Z

En resumen en la multiplicación de núemros enteros se aplica la regla conocida como “regla de los signos” que sintetizamos en siguiente recuadro:


3 . (- 2) = - 6 ; ( -3) . ( -8) = 24 ; ( -5) . 5 = -25
División en Z

Para determinar el signo del cociente cociente, en resumen, aplicamos la siguiente regla de signos:


8 : -2 = -4 ; -10 : - 5 = 2; -6 : 3 = -2
Hasta acá nuestro post del día, quedan como asignación al lector investigar respecto a la potenciación en Z, así como la información de las operaciones suma, multiplicación y potenciacíon.
Los espero en nuestro próximo encuentro. Saludos amigos!!