Hi Everyone,

In this post, I would like to investigate possible Steem rewards curves. I have discussed Steem Economics in several posts. I have only ever very briefly touched on the rewards curve for content creators. I am approaching the subject today because of the recent posts by @steemitblog and @vandeberg. You can access these posts using the following links.

The @steemitblog post outlines a plan proposed by @trafalgar. This plan involves making three key changes. These changes are:

Moving from a linear rewards curve to a convergent linear rewards curve.
Increasing the percentage of rewards that are distributed to curators.
Create a separate “downvote pool”.

I have previously discussed both increasing curation rewards and a downvote pool. Therefore, I will not touch on these proposed changes in this post. If you are interested in my opinions on both of these proposed changes, you should read the following posts in my ‘Steem ecosystem in disequilibrium’ series. Part 2 and Part 5 contain the most discussion. The other parts provide greater context.

Is the Steem ecosystem in disequilibrium? (Part 1 – Witnesses)

Is the Steem ecosystem in disequilibrium? (Part 2 – Content Creators and Curators)

Is the Steem ecosystem in disequilibrium? (Part 3 – Applications and Services)

Is the Steem ecosystem in disequilibrium? (Part 4 – Passive Income)

Is the Steem ecosystem in disequilibrium? (Part 5 – Combination of solutions)

The @vandeberg post focuses entirely on the proposed ‘convergent linear rewards’ curve. The post explained in some detail how such a curve would work. I will include this proposed curve as part of the discussion and analysis presented in this post.

How does a rewards curve function?

The reward curve determines how votes distribute the rewards pool. Steem currently uses a linear rewards equation for content creators. What this means is that the rewards to the content creator from your vote does not vary depending on how others voted. If a non-linear equation is used, the rewards to the content creators from your vote will vary depending on the value of votes from other stakeholders (reward shares distributed by votes). For example, if your post has a value of 50 STU (Steem Token Units) my vote will increase the value of your author reward by more, than if your post was worth only 5 STU. This can be demonstrated more clearly using graphs.

Types of reward curves and what they will look like

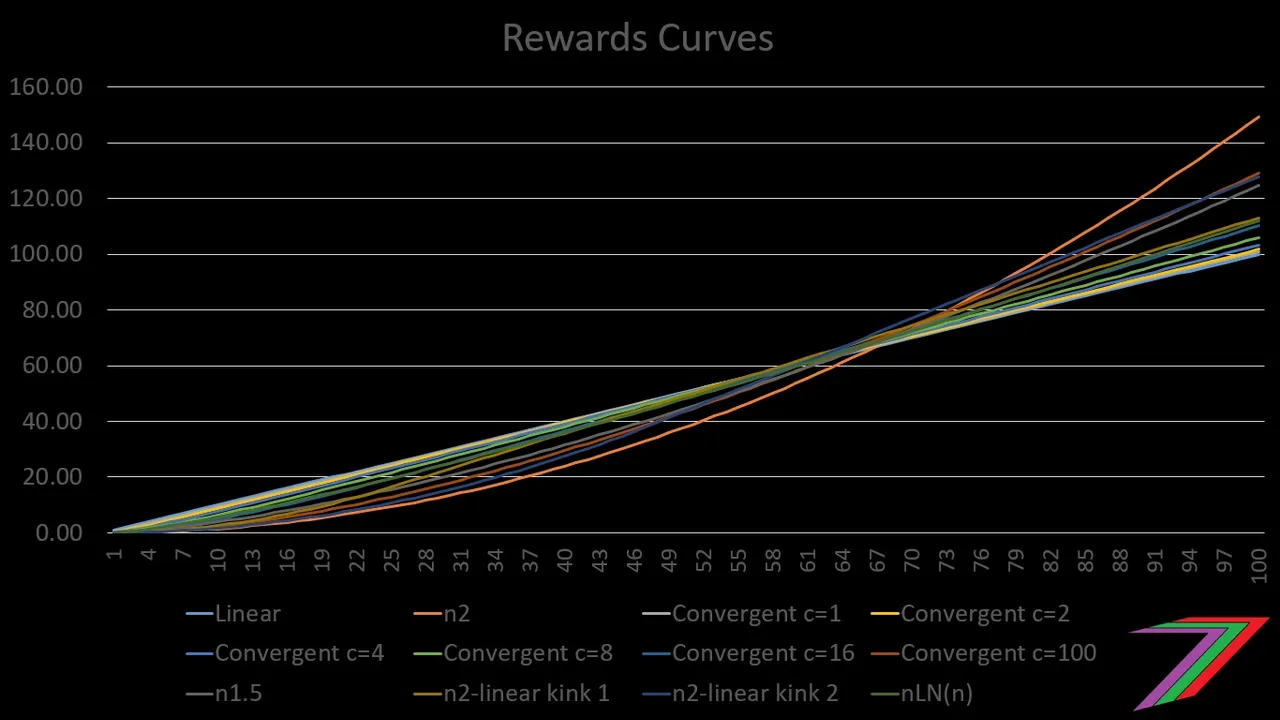
There are many possible rewards curves. There is the linear reward curve and there are almost endless possibilities of non-linear curves. We could have N-squared, N-cubed, N^1.5 or any other power. We could have exponential curves or logarithmic curves. We could have the proposed ‘convergent linear rewards’ curves and any number of variations of that.

I will start with the ‘convergent linear rewards’ curve since it is being considered by Steemit Inc. The proposed formula is expressed as follows:

N^2/(N/c+1)

Where: N is the unadjusted reward shares and c is a parameter that influences the non-linearity of the equation

N-squared forms part of the formula but the most important parameter in the formula is ‘c’. As ‘c’ becomes larger (approaches infinity), the formula more closely resembles N-squared. As ‘c’ becomes smaller (approaches zero), the formula more closely resembles the linear formula. Figure 1 compares linear, N-squared and various versions of the ‘convergent linear rewards’ curve with different values of ‘c’.

Figure 1: Convergent linear rewards curve

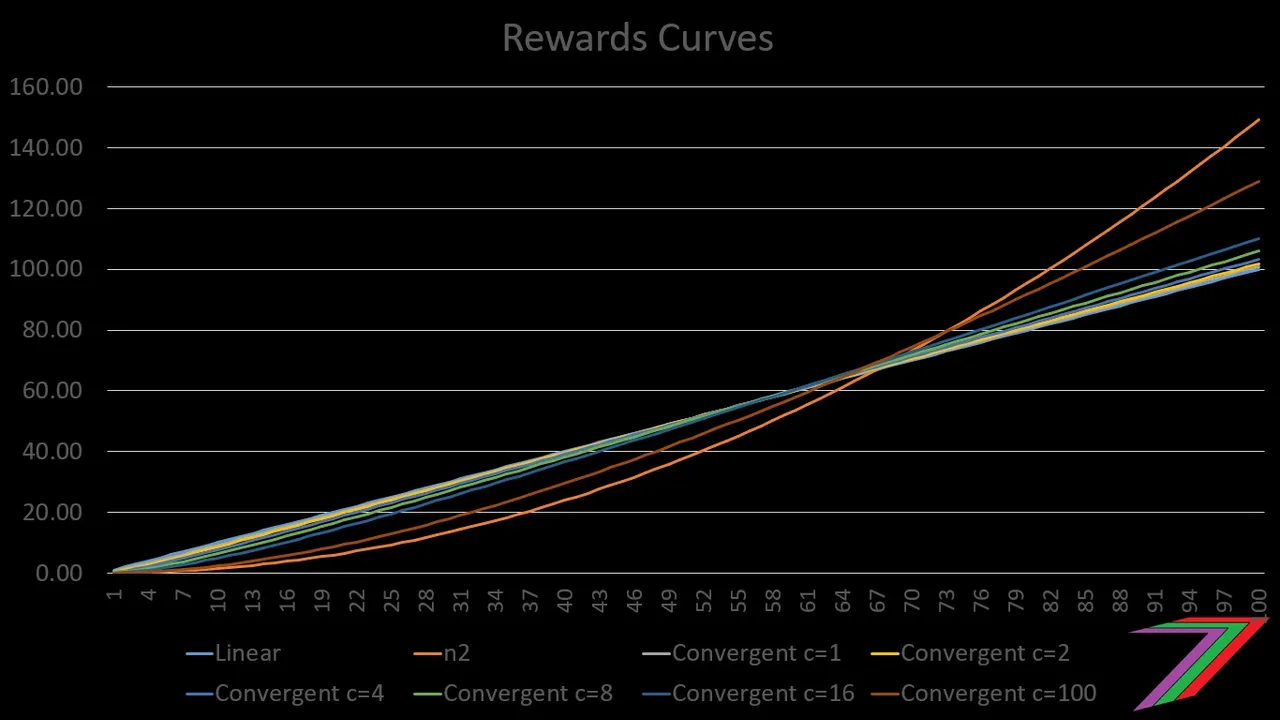
Note 1: The y-axis is the adjusted post rewards and the x-axis is the unadjusted post rewards. These axes apply to all rewards curve graphs in this post.

Note 2: The shapes of the curves in these graphs are not exact representations of payouts. These will vary depending on the size of the rewards pool and distribution of votes.

As can be observed from Figure 1, the ‘convergent linear rewards’ curve is very similar to a linear curve. A high value for ‘c’ such as 100, starts to shape the rewards curve in a similar shape to the N-squared curve.

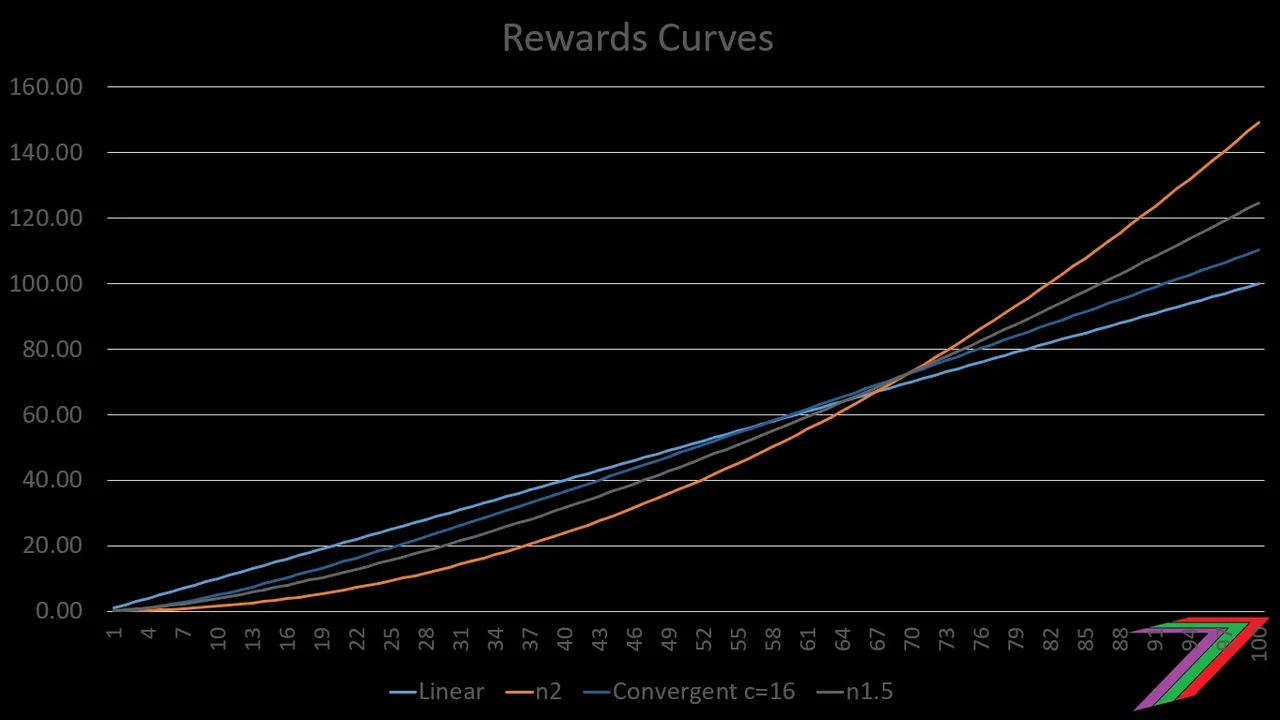
Another option for a non-linear curve is N^1.5. This curve is flatter than N-squared but creates a similar effect. In Figure 2, N^1.5 is compared with N-squared, linear, and the ‘convergent linear rewards’ curve where ‘c’ equals 16.

Figure 2: N^1.5 Rewards Curve

N1.5.jpg

Linear and non-linear equations can be combined to create a linear-non-linear hybrid rewards curve. The place of the ‘kink’ will determine if the curve more closely resembles a linear rewards curve or a N-squared rewards curve. Figure 3 contains examples of curves with both linear and N-squared components to it.

Figure 3: Linear and N-Squared

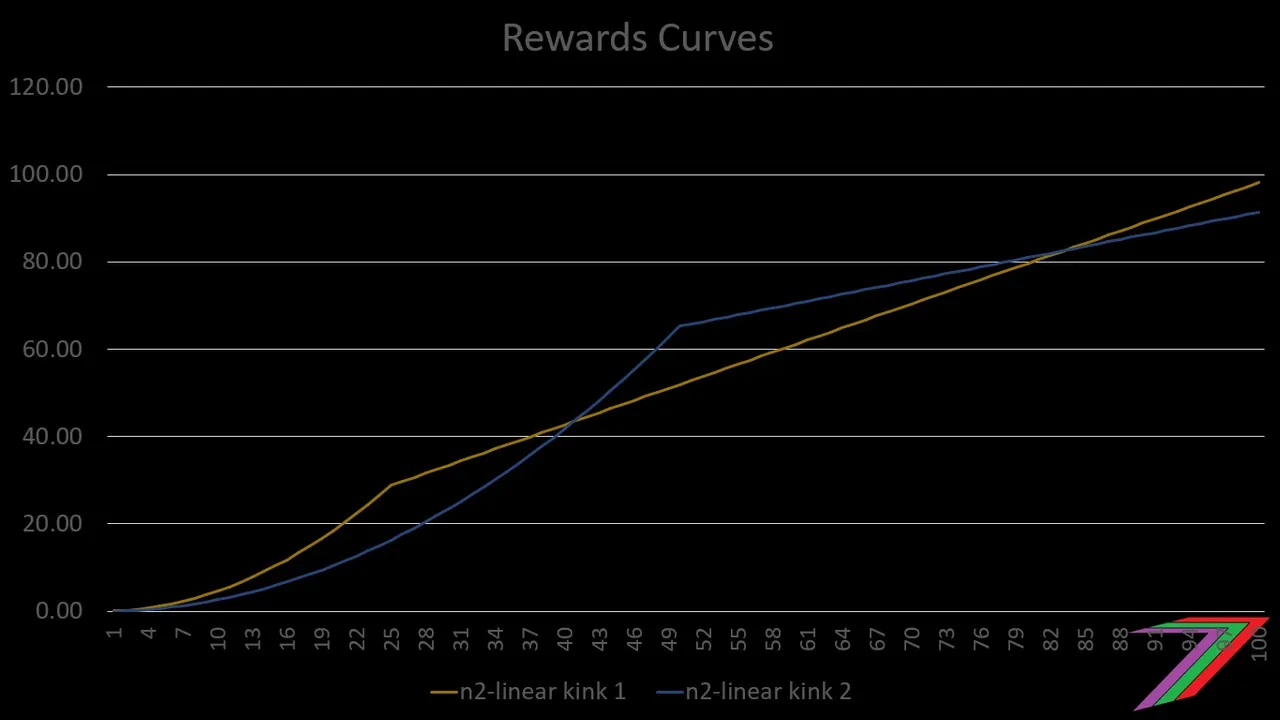
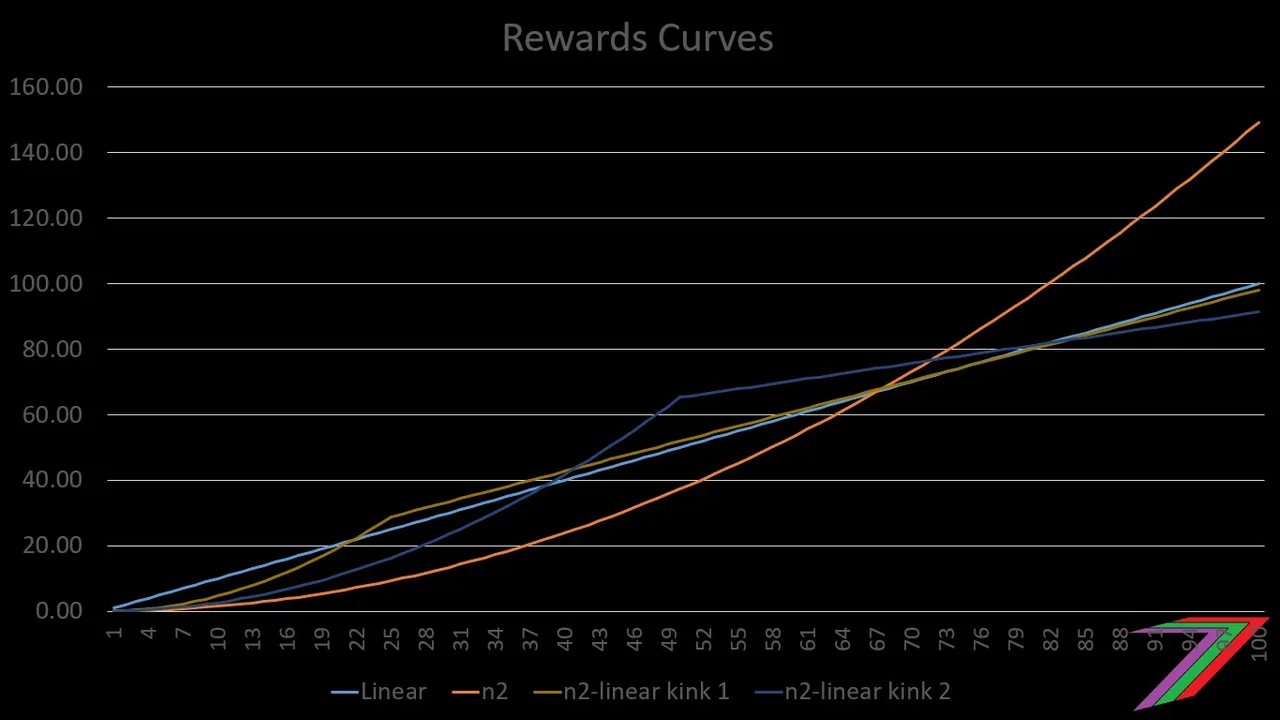
Figure 4 compares the linear-non-linear hybrid rewards curves to N-squared and linear rewards curves.

Figure 4: Comparing Linear and N-Squared hybrid to other curves

Another interesting non-linear curve is created by multiplying the natural logarithm of ‘N’ with ‘N’ (nLN(n)). This curve is a very gentle non-linear curve compared with N-squared. Figure 5 compares the nLN(n) curve with the N-squared curve and the linear curve.

Figure 5: Comparing nLN(n) with N-squared and linear curves

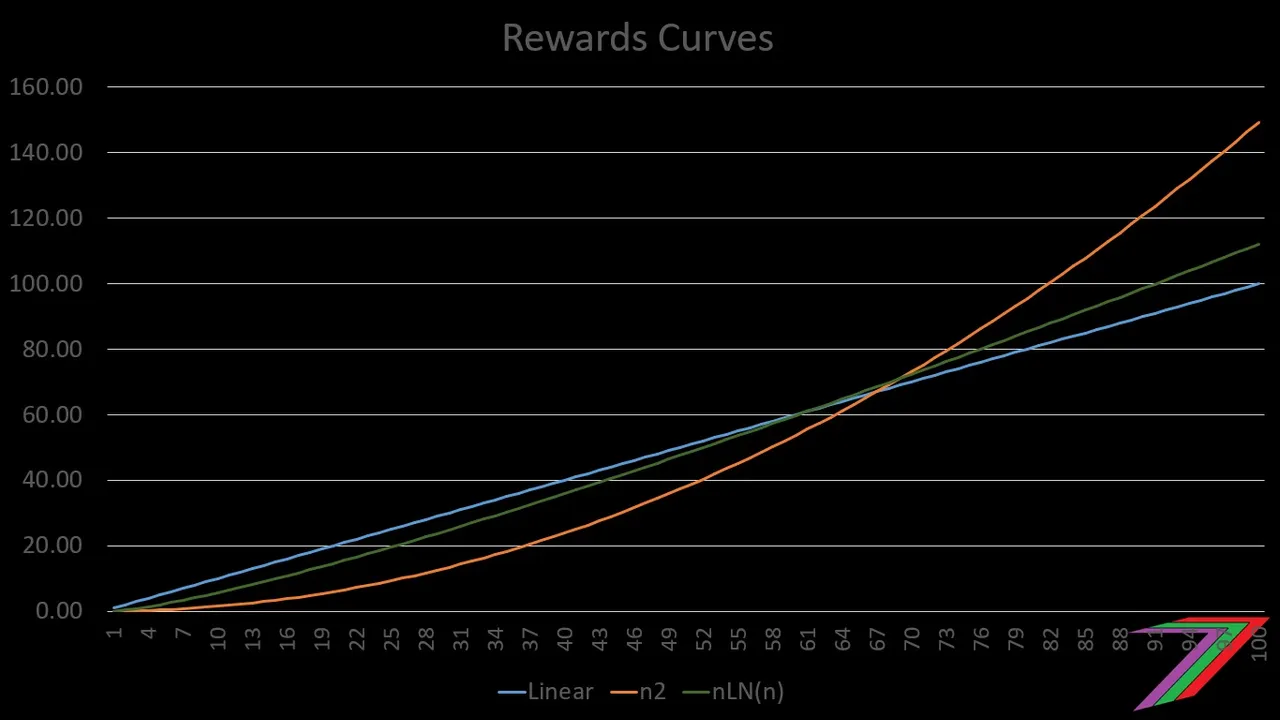
These are just a few of the possible rewards curves. Linear and N-Sqaured currently sit at the extreme ends of the rewards curve spectrum that have been considered as possible rewards curves. The other types of curves fit somewhere in-between these two. The convergent linear rewards curve appears to be the most flexible in regards to the shape it can take based on the ‘c’ parameter in the formula.

Does the rewards curve make a difference?

Steem previously used an N-squared rewards curve. The N-sqaured rewards curve was unpopular with some people as a few content creators benefited greatly while most earned very few rewards. Changing to linear rewards was deemed to add more fairness to the system.

What behaviour do we wish to encourage?

Before we consider what type of rewards curve is favourable, we should consider the type of behaviour we want to encourage on the platform.

Steem is intended to use a proof-of-brain approach to reward its users. This applies to both content creators and curators. The content creators that create the most popular content should earn the highest rewards. The curators that contribute most to content discovery should earn the highest rewards.

What behaviour is most incentivised?

For a stakeholder, the highest returns are from self-voting, circle-voting, vote selling, and delegating to bots. For a content creator, the highest returns are from circle-voting and vote buying. All of the above actions contribute very little to the Steem ecosystem and do not align with the behaviour we wish to encourage.

Could changing the rewards curve possibly solve the mismatch between desired actions and incentivised actions?

To have a better idea. Let’s summarise what linear and non-linear rewards curves are likely to incentivise. Table 1 compares linear with non-linear rewards curves.

Table 1: Possible behaviour encouraged by linear and non-linear rewards curves

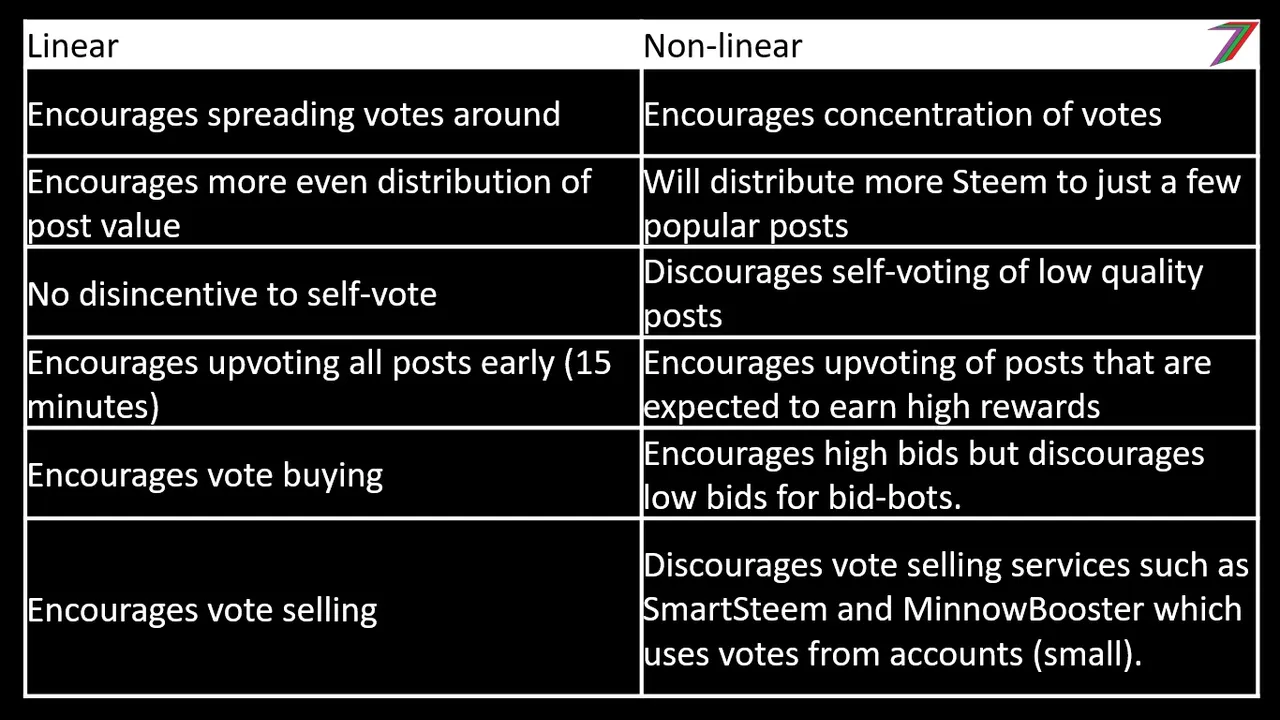
If Steem switches to a non-linear rewards curve, I can predict the following could happen.

Self-voting will be reduced.
Vote selling through vote services such as SmartMarket and MinnowBooster will be reduced.
More Steem will be delegated to bid-bots.
There will be less small bid-bots and more large bid-bots.
There will be more users making high bids with several large bid-bots to take advantage of a higher return created by the non-linear curve.
The median payout per post will fall.

Logic supporting my predictions

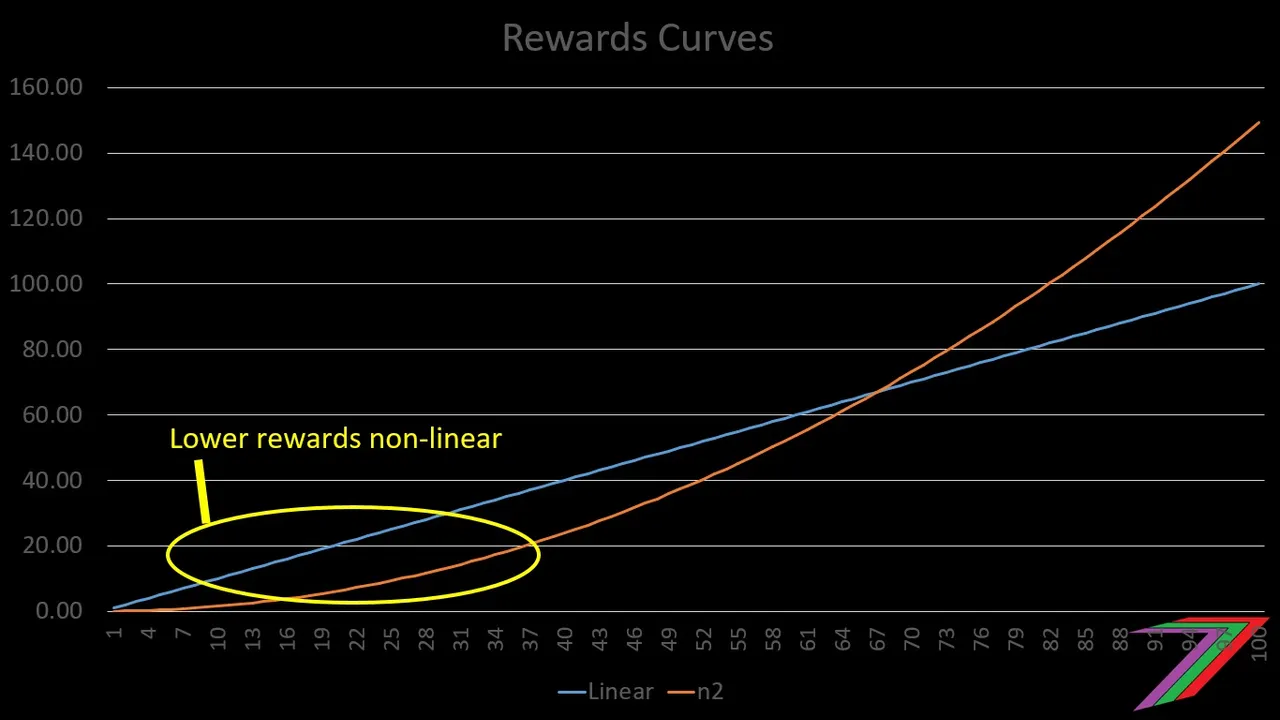
Returns on self-voting comments, spam, and low quality posts will be reduced. These types of posts will be earning at the lower flatter end of the non-linear curve. The same argument can be made for earnings on individually sold votes and small bid-bots. See, the graph in Figure 6.

Figure 6: Lower rewards for self-voting and vote selling

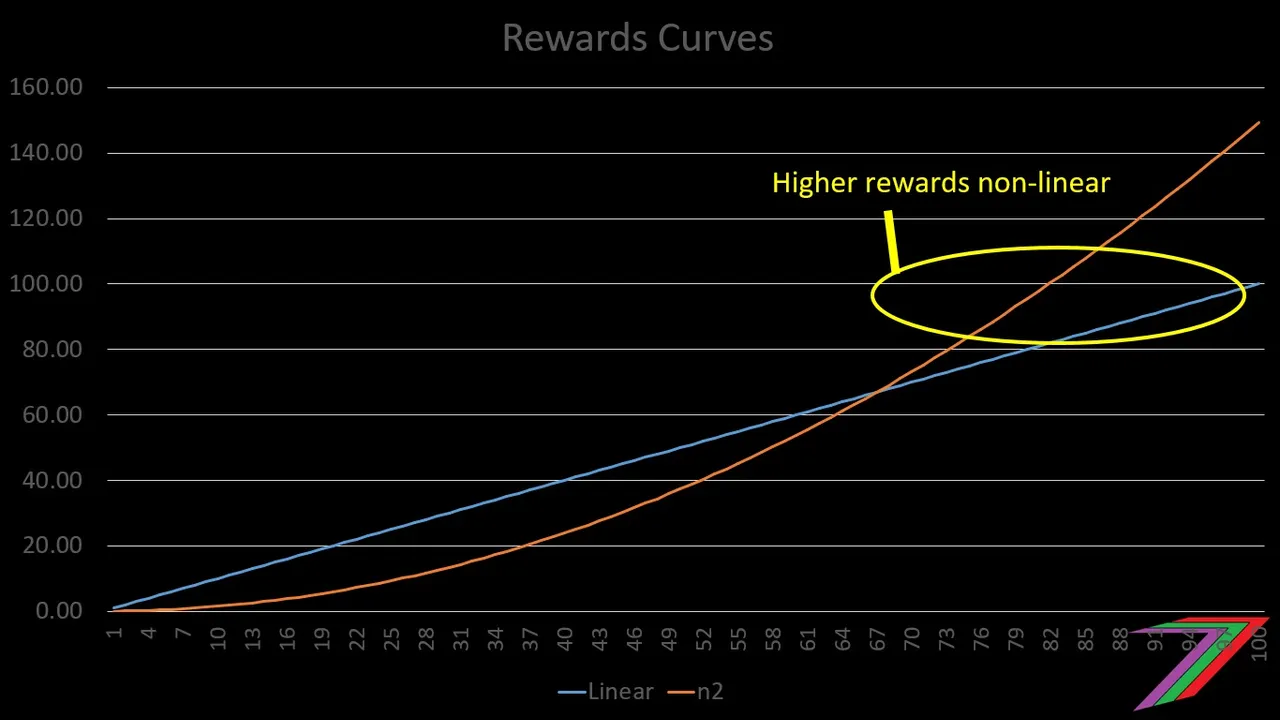
Larger bid-bots are likely to thrive with non-linear rewards. This is because vote buyers can buy very large votes that will put the rewards of their post in the top steeper half of the rewards curve. See, the graph in Figure 7.

Figure 7: Higher rewards for those buying votes from large bots

Therefore, high bids are likely to produce much higher returns on investment (ROI) than lower bids that do not move the payout of the posts into the top portion of the curve. The posts of the high bidders are also likely to attract frontrunners who will benefit greatly from the high curation rewards generated by the bots, which will be further magnified by the non-linear rewards curve.

The median payout per post will fall simply because of the nature of non-linear curves described in this post. The non-linear curve takes from low valued posts and gives to the higher valued posts. The fall in the median payout will hurt the new users that have yet to establish a following. These new users may also struggle to obtain a following without the use of bots to provide their posts with some visibility.

What is the likely net effect?

There are some likely positive outcomes from implementing a non-linear rewards curve. Reduced self-voting being the biggest of those. A non-linear rewards curve such as N-squared would be the most successful against self-voting.

There are some likely negative outcomes, such as skewing rewards to just a few posts as well encouraging excessive vote buying from bots. Non-linear rewards such as the ‘convergent linear rewards’ curve with a low value for ‘c’ may not create that problem. However, it may not be sufficient to discourage self-voting either.

Changing to non-linear rewards curves as part of a broader strategy

Steemit Inc are considering changing the rewards curve as part of a broader strategy and not as an isolated change. This is important as changing the rewards curve is not required to be a complete solution. A non-linear rewards curve could reduce self-voting and the other solutions such as high curation rewards and downvote pool could reduce bot use. However, high curation rewards and non-linear rewards could further encourage users to vote for posts from the same users. Circle-voting could become the dominant strategy for many users.

My opinion

I have expressed that I am in favour of both higher curation rewards and a separate downvote pool. I also believe that these two approaches alone are not likely to be sufficient to improve the rewards mechanisms on Steem substantially. I would also include curation rewards to be paid out in both SBD (Steem Blockchain Dollars) and Steem Power. This should align with the decision of the content creator rather than all curation rewards paid out as Steem Power. I also believe delegation contracts are necessary to utilise higher curation rewards. Delegating to curators or DApps should be a viable alternative to delegating to bid-bots.

In regards to linear or non-linear rewards curves, I do not believe a change is necessary. Changing back to the N-squared rewards curve could do more harm than good as highlighted by my predictions. Changing to the ‘convergent linear rewards’ curve with a low ‘c’ value may not have much or any effect on behaviour. Therefore, this change may not be worth implementing. Implementing non-linear rewards curves could be better to suited for Smart Media Tokens (SMTs). This would be less risky to the Steem ecosystem as well as enable experimentation with different curves with different parameters. I do not think anyone has a confident answer as to what formulae or parameters should be used to create the optimal rewards curve.

If you want to read any of my other posts, you can click on the links below. These links will lead you to posts containing my collection of works. These posts will be updated frequently.