Steem pays curation weighted by sqrt( P + R ) - sqrt( P ), where P is the rshares of the previous votes and R is the shares of the current voter. But, curation rewards are multiplied by min( 1, T/15 ), where T is the number of minutes past the post that the voter acts. (I'm not 100% clear whether it's just that voter or the entire curation reward.)
We can build a simplified model of this as an N-player game where all players have equal voting weights. The pure strategies then consist of a vector of N-1 numbers: at what minute to vote, given that "i" players have upvoted already. (If all other players have already voted, then wait for the 15 minutes mark.)
For example, in a 5-player game the strategy [13,14,15,15] says to vote at 13 minutes if there are 0 votes, 14 minutes if there is 1 vote, and at 15 minutes if there are 2, or 3 votes already. This gives 16^4 = 65536 pure strategies.
I was thinking about whether it would be feasible to simulate this game using fictitious play, but that number of pure strategies leads to a very big matrix, and the simplifying assumption that all opponents use the same pure strategy probably leads to incorrect results, so we would end up with an even larger number of pure-strategy evaluations to iterate on a mixed strategy.
However, I think that we can look for Nash Equilibria in the game. These are pure strategies where no player can individually make a move that improves their payout.
In the 2-player game, we can easily see that [15],[15] is not a Nash equilibrium. A player who moves to (14) will see an increased payout. The payout for being first is 0.707 of the curation rewards, while second is 0.293. Voting at minute 14 is worth 0.660 (=0.707 * 14/15) when the other player votes at minute 15, compared to an expected fair split of 0.500 if you both vote at minute 15.
A quick spreadsheet model:
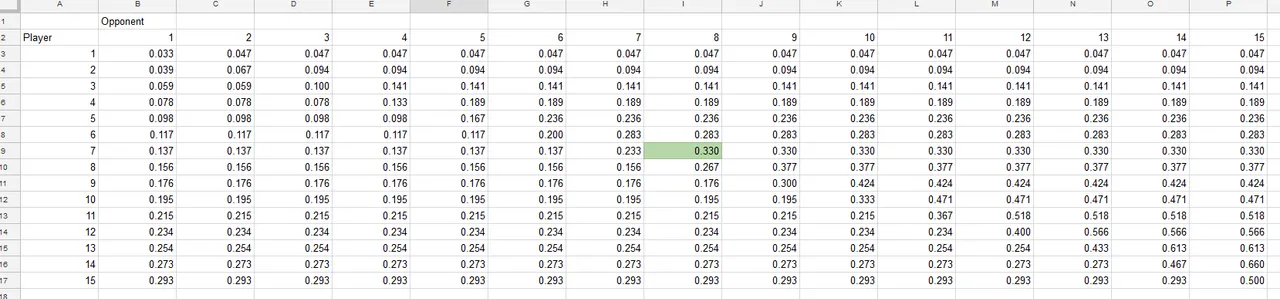
Because the game is not zero-sum, equilibria are not guaranteed to exist and a quick eyeball search didn't turn up any. None of the diagonals are; when they are high, the player or his opponent is better off switching to a lower value, and when they are low, the player is better off giving up and voting at 15 minutes.
[9],[9] is better than [15],[9] for the player, but [8],[8] is worse for the player than [15],[8]. But the opponent is tempted to move later. So, there do not appear to be any pure-strategy equilibria. (And it's way to late for me to calculate the mixed-strategy equilibrium.)
Update
The spreadsheet above assumed that the second player would still vote rather than wait for minute 15. The one below fixes that:
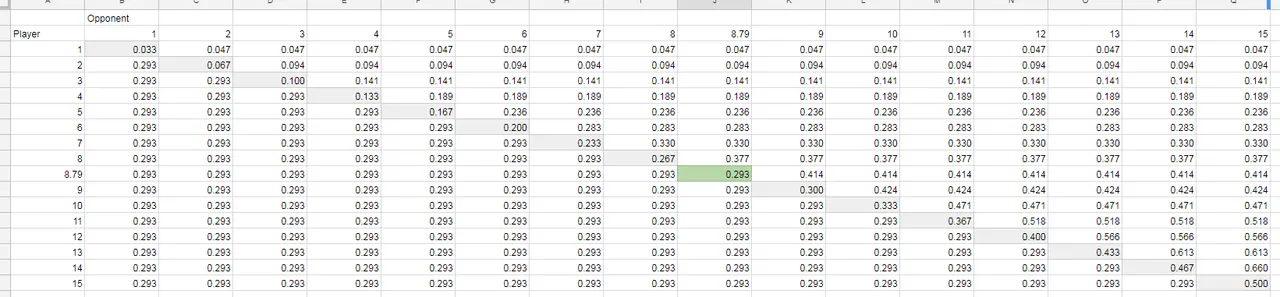
I also calculated the time value that would make the player indifferent between tying and waiting, which is 8.79 minutes. But tying at this value still makes the player motivated to try for 8 minutes instead, so (8.79,8.79) is not an equilibrium.