Discriminant and the Nature of Roots (Solutions) of a Quadratic Equation

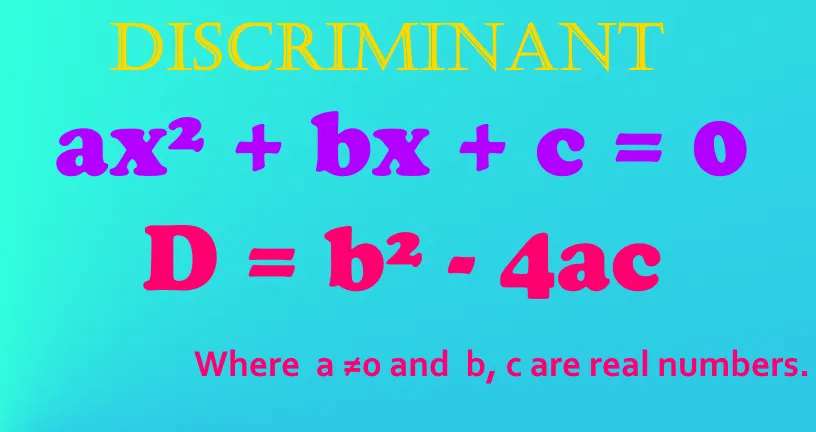
The relation between the coefficients of standard quadratic equation ax² + bx + c = 0 is known as discriminant. It is denoted by “D”. Discriminant is the part of the quadratic formula.

There is the following formula (relation) to find discriminant of a quadratic equation;

D = b² - 4ac Where a ≠0 and b, c are real numbers.

Discriminant gives very important information about the root(s) or solution(s) of a given quadratic equation. Please note that a quadratic equation can have maximum of two roots. Also it can have only one root or no roots.

By determining the discriminant we can predict the nature of roots of a given quadratic equation without solving it. Nature of roots means if the equation has two distinct real roots, only one real root or no real roots. Word real means Real Numbers.

For example; 2x² + 3x – 5 = 0 is the given quadratic equation. Let’s determine it’s discriminant “D”.

I will compare the given equation with the standard quadratic equation ax² + bx + c = 0 to find the values of “a”, “b” and “c” as shown below;

a = 2, b = 3 and c = -5

We know D = b² - 4ac

D = (3)² – 4(2)(-5)

D = 9 + 40

D = 49 which is >0

As D>0, the given equation has two distinct real roots or solutions.

There are other two scenarios depending upon the values of Discriminant are given below;

If D = 0, there is only one real root or solution

If D<0, there are no real roots or solutions. Imaginary roots are possible.

Let’s comprehend all the above; For the Standard quadratic equation ax² + bx + c = 0; D = b² - 4ac