Welcome to my new article. This time, the article will be completely scientific, so you'll need to handle some mathematical tools. Hope you like it, and thank you for reading.
Introduction
In this article we're going to learn what is Thermal Radiation. Also, we will proceed to the explanation of the Stefan-Boltzmann law, detailing the way to verify it. Finally, we will attach studies carried out to, effectively, verify this law.
Again, I think it's necessary to have some knowledge to understand what is explained below, since not all expressions will be 100% detailed
Theoretical Framework
Thermal Radiation and Emissivity
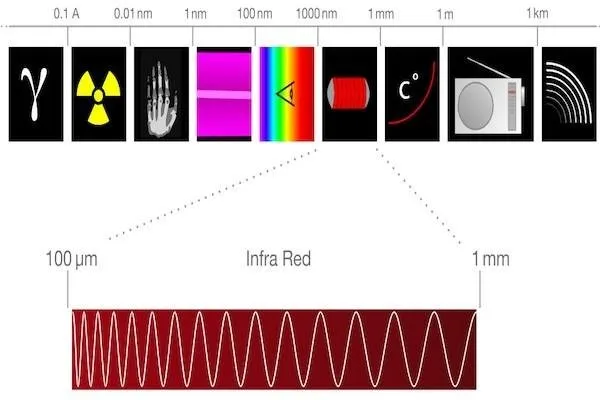
The termal radiation is a type of radiation emitted by a body, depending on its temperature, in the form of electromagnetic waves. This type of EM waves have a wavelength that varies between 0.74 μm and 4 μm. So, it is a kind of infrared radiation.
One must proceed, then, to the definition of emissivity, a variable that indicates in what proportion a body emits thermal radiation. This variable is measured by the emissivity coefficient ε, which indicates the quotient between the radiation emitted by a surface and the radiation that would be emitted if the object where a black body. ε is a dimensionless variable.
Source
Black body
Black body is defined as an ideal body that does not reflect radiation incident on it, that is, all the radiation that falls from the outside on its surface is absorbed by it, and all the radiation that comes from the inside is emitted. This type of ideal body is characterized with a coefficient of emissivity ε=1. Actually, in nature there are not real black bodies, since the best approximation to this body type reflects at least 1% of the incident radiation.
Stefan-Boltzmann Law
The Stefan-Boltzmann Law relates the amount of energy per unit of area and time emitted by a surface to the temperature by the following expression:
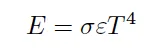
where we can identify the E as the energy, σ is the Stefan-Boltzmann constant, ε is the emissivity coefficient and finally T is the temperature.
What this law tells us is that the energy that is emitted by a body is directly related to the fourth power of the temperature.
If we consider that we're studying a black body (ε=1), the expression takes this form:
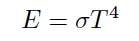
We can also consider the black body radiation as if it were an ideal gas of photons in thermal equilibrium.
If we perfom a study from the thermodynamic point of view, considering the internal energy per unit volume u= U/V = u(T), we would arrive at the following expression for the internal energy:
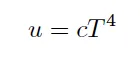
so the law is verified mathematically.
The calculations made to get to this expression won't be published to facilitate the understanding of the article, but if someone wants to see them I have no problem on publishing them later
Experimental verification of Stefan-Boltzmann Law
Instruments used
To perfom the experiment, I used the following instruments
- Oven with a cylindrical cavity == Horno
- Thermometer == Termómetro
- Thermopile == Termopila
- Micro-Voltmeter == Microvoltímetro

Instruments
Thermopile
For a coherent development of the next section, we need to summarize how a thermopile works.
This device detects the thermal radiation coming from a surface that is at temperature T, in an enviroment at temperature To, and will provide a voltage with the next form (being β a constant):
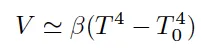
In this case, T was so much bigger than To, so we can ignore the term To in the equation.
Experimental development
The experiment is relatively simple. We only have to connect the oven and the microvoltmeter, then turn on the thermometer and take notes of how many microvolts does the microvoltmeter reads for some temperatures.
The thermopile will receive the radiation from the oven and will produce the voltage that will be read by the microvoltmeter.
The measurements will be taken from 200ºC to 320º in 10ºC intervals.
To verify that the energy is effectively related to the fourth power of the temperature, we will make a linear regression of the data, where we will represent the neperian logarithm of the measured voltage versus the neperian logarithm of the temperature.
Finally, the adjustment will give us a straight line, where the slope should take a value "α"close to 4, according to the fourth power of the temperature.
Results
The results of the data collection are the following, where V is the voltage and T the temperature.
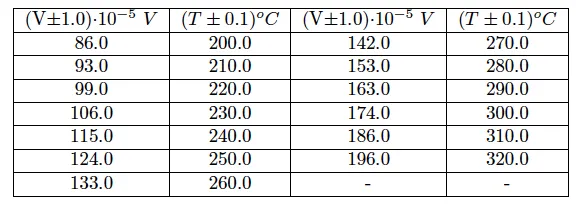
Data collection
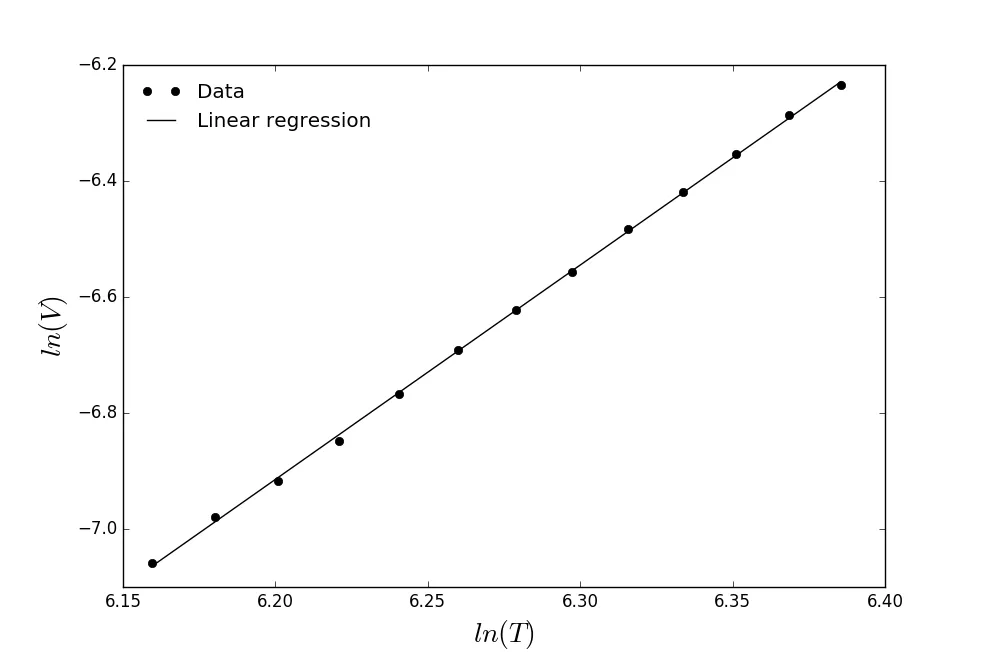
Graphical representation of the data
The straight line has an equation with the form of
and in this case, our α = 3.69 == 3.7.
Therefore, we can conclude this article by stating that Stefan-Boltzmann's law is valid, since the value obtained for α is quite close to 4.
Why it was not α=4 exactly?
We must remember that in order to carry out this experiment we made an approximation that the cavity of our oven acts as a black body, without knowing in what percentage this object acts as such.
On the other hand, we have to take into account that we have not taken into account the ambient temperature, since it was much lower than that of the oven, leading to errors in the calculations.
Despite this, the results obtained are clearly satisfactory.
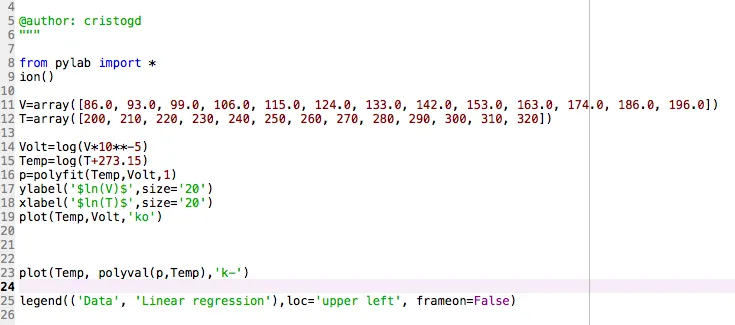
Python code used for the calculations
References
All the measurements were taken by me.
[1] https://es.wikipedia.org/wiki/Ley_de_la_inversa_del_cuadrado
[2] https://es.wikipedia.org/wiki/Cuerpo_negro
[3] https://es.wikipedia.org/wiki/Emisividad
[4] https://es.wikipedia.org/wiki/Radiacion_termica
[5] http://www.sc.ehu.es/sbweb/fisica/cuantica/negro/radiacion/radiacion.htm