The astronomer Galileo Galilei observed in 1623 that the entire universe "is written in the language of mathematics", and indeed it is remarkable the extent to which science and society are governed by mathematical ideas. It is perhaps even more surprising that music, with all its passion and emotion, is also based upon mathematical relationships. Such musical notions as octaves, chords, scales, and keys can all be demystified and understood logically using simple mathematics
The Connection Between Music and Mathematics
The famous Greek philosopher and mathematician Pythagoras once said, “There is geometry in the humming of the strings, there is music in the spacing of the spheres.” Although some may interpret this statement as mere poetry, Pythagoras was actually making a direct statement on the relationship between music and mathematics. You see, music is entirely intertwined with mathematics, so much so that even a basic major chord can be described mathematically.
History of Studying Music & Mathematics
It’s common knowledge that music has long played for performance and pleasure, yet the study of music, particularly its relation to mathematics, has been going on for equally as long as music for performance. From Greeks to Egyptians to Indians to Chinese, nearly every ancient civilized culture has examined the connection between music and mathematics. Famous philosopher Plato was known to have an extreme interest in music, particularly harmonies, and helped highlight their importance within both an individual and society. Plato wasn’t the only philosopher who found the importance of studying the relationship between music and mathematics – ancient Chinese philosopher Confucius is said to have stated that within music are a number of fundamental truths.

INTRODUCTION
Music theory has no axiomatic foundation in modern mathematics, yet the basis of musical sound can be described mathematically (in acoustics) and exhibits a remarkable array of number properties.
A little Physics! And some Musical Background
Pitch: Wave frequencies
Sound is a wave, and that the frequency of the sound is what defines the note. A sound wave creates minute pockets of higher and lower air pressure, and all the sounds we hear are caused by these pressure changes. With music, the frequency at which these pockets strike your ear controls the pitch that you hear.
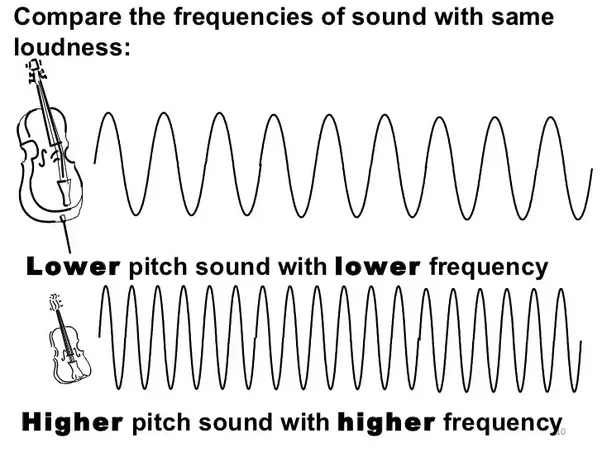
But what is frequency? It is a repetition. Imagine, for example, a bicycle wheel spinning. If this wheel completes a turn in 1 second, we say that the frequency of this wheel is “one turn per second”, or “one Hertz”.
Nice, but where is the connection with sound? Well, sound is a wave, and this wave oscillates with a certain frequency. If a sound wave completes one oscillation in one second, its frequency will be 1 Hz. For each frequency, we will have a different sound (a different note). A note, for example, corresponds to a frequency of 440 Hz.
When we listen to music, we assume that we are hearing a song or a collection of notes, but what our brains are actually processing are sound waves. For example, when a note is played, sound waves travel from an instrument and reverberates on our ear drums, and it’s the frequency of this sound wave that tells our brain which pitch or note is being played .
Mathematics in music

Octaves
No musical notes fit together better than those which are exactly one octave apart. Pairs of notes like Middle C and High C. Or Middle G and High G. Such pairs arise constantly in popular music, as in the first two notes of the third line of Happy Birthday.
Often in a symphony, one instrument (like a violin) plays a note one octave above that of another instrument (like a double bass). Piano arrangements inevitably include the same note at different octaves. What is it that makes notes one octave apart fit together so well? Consider High C, the note which is exactly one octave above Middle C.
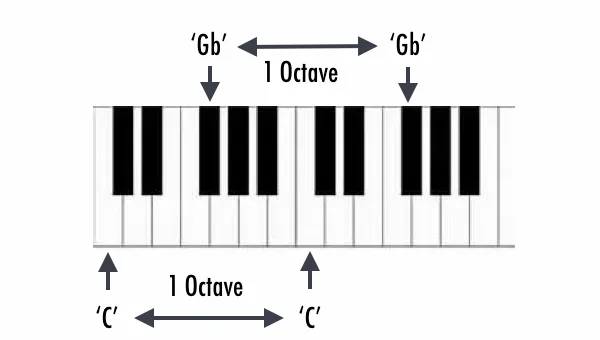
It was observed that when a frequency is multiplied by 2, the note still the same. For example, the A (440 Hz) multiplied by 2 = 880 Hz is also an A, but just one octave above. If the goal was to lower one octave, it would be enough just dividing by 2. We can conclude then, that a note and its respective note have a relation of ½.
Very well, before going on, let’s return to the past, to the Ancient Greece. In that time, there was a man called Pythagoras that made really important discoveries to Mathematics (and music). This that we showed about octaves, he discovered “playing” with a stretched string. Imagine a stretched string tied in its extremities. When we touch this string, it vibrates (look the drawing below):

Pythagoras decided to divide this string in two parts and touched each extremity again. The sound that was produced was the same, but more acute (because it was the same note one octave above):

Pythagoras didn’t stop there. He decided to experience how it would be the sound if the string was divided in 3 parts:

He noticed that a new sound appeared; different from the previous one. This time, it wasn’t the same note one octave above, but a different note, that was supposed to receive another name. This sound, besides being different, worked well with the previous one, creating a pleasant harmony to the ear, because these divisions showed till here have Mathematics relations 1/2 and 2/3 (our brain likes well defined logic relations).
In principle, we could keep increasing the octaves, and doubling the frequencies, forever - but after a certain point, the notes would be so high that only dogs could hear them.
Chord & Scale
This combination of variety and consistency is just what is required to produce the C Major chord - one of the most pleasing sounds known to humanity, and the basis of multitudes of tunes from Mendelssohn to Metallica.

Key
Changing a song's key raises or lowers all the notes by the same amount. This change might make the song more convenient to play on a particular musical instrument, or more comfortable for a vocalist to accompany. If done properly, the key change should have essentially no effect on the way the song "sounds" - it should be just as recognisable, just as lovely, and just as catchy, in the new key as in the old. Indeed, it should be exactly the same song, just performed at a higher or lower pitch.

Going bit depth on Mathematics of Scales
A musical scale is a discrete set of pitches used in making or describing music. Many peoples and cultures created their own music scales.
One example is the Chinese people, which began with the idea of Pythagoras (using strings). They played C in a stretched string and then divided this string in 3 parts, like we showed before. The result of this division was the note G. Noticing that these notes had a harmony; they repeated the procedure starting in G, dividing again this string in 3 parts, resulting the note D. This note had a pleasant harmony with G and also with C. This procedure was then repeated starting in D, resulting in A. After that, starting in A, they got E. When they repeated this procedure of dividing the string in three parts once again, resulting in B, there was a problem, because B didn’t fit well when played with C (the first note of the experiment). Actually, these notes were really close one another, what caused a “sound discomfort”. Because of this, the Chinese finished their divisions getting the notes C, G, D, A and E, taking B aside. These notes served as base to Chinese Music, making a scale with 5 notes (Pentatonic). This Pentatonic Scale, for being pleasant and consonant, represented very well the Oriental Culture, which was always connected to harmony and stability. Since its creation until today, the Pentatonic Scale represents a good option to melodies, But let’s return to the subject of notes and frequencies, because we just showed 5 notes of the scale.

The Mathematics of 12 notes
The western music, which works with 12 notes, did not discard the note B as the Oriental Culture did. The western people observed that the notes C and B were close one from another and decided to create a more comprehensive scale. In this scale, all the notes should have the same distance one from another. And this distance should be the interval that had between C and B (one semitone). In other words, between C and D, for example, should exist an intermediate note, because the distance between C and D (one tone) was bigger than the distance of C and B (one semitone). Through an analysis of frequency, it was discovered that multiplying the frequency on the note B by the number 1.0595 we would arrive in the frequency of C.
Frequency of B: 246.9 Hz
Frequency of C: 261.6 Hz
Multiplying the frequency of B by 1.0595 we will have:
246.9 x 1.0595 = 261.6 Hz (the note C).
As the goal is to keep the same relation (distance) to the other notes, we will use this procedure to discover which note will come after C. Multiplying the frequency of C by 1.0595:
261.6 x 1.0595 = 277.2 Hz (the note C sharp)
Repeating this procedure to see what comes after C sharp:
277.2 x 1.0595 = 293.6 Hz (the note D)
Notice that following this logic, we can create all the chromatic scale! In other words, after multiplying the frequency of C by the number “1.0595” twelve times, we will return to C. This is possible because “1.0595” corresponds to the result of the square root 12√2. Notice that 12√2 multiplied 12 times by itself is (12√2)12 = 2. And we already saw that a note multiplied by 2 is itself one octave above.
Now we can clearly see that these numbers didn’t come by chance. The goal since the beginning was dividing a scale in 12 identical parts, in a way that the last note return to be the first.
Logarithm in Music
We will not go in many details, but those who know a little bit about Math have noticed that we worked here with the logarithm of base 2. Because of this, the makers of piano put the form of a logarithm graphic in the piano body, to make a reference to this Musical Mathematics Discovery. Check it:
Example of a Logarithm graphic: 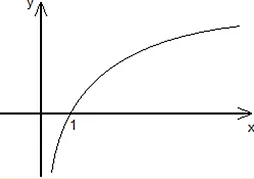
Piano body:

There are many other Mathematical explanations to many questions about music, but to show them here it would be necessary to talk about advanced topic in Mathematics, like Fourier series, Riemann Zeta Function, etc.we will not go more deeper. The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory. Some composers have incorporated the golden ratio and Fibonacci numbers into their work.
Set theory
Musical set theory uses the language of mathematical set theory in an elementary way to organize musical objects and describe their relationships. To analyze the structure of a piece of (typically atonal) music using musical set theory, one usually starts with a set of tones, which could form motives or chords. By applying simple operations such as transposition and inversion, one can discover deep structures in the music. For example, the pitch classes in an equally tempered octave form an abelian group with 12 elements. It is possible to describe just intonation in terms of a free abelian group.
Symmetry
Music is really just a way of applying symmetry to events in time. See this delightful paper by Vi Hart about symmetry and transformations in the musical plane.
Discrete mathematics
The pitch continuum is, well, continuous, but tuning systems and scales are discrete. The voice, fretless stringed instruments and trombones produce continuous pitches. Keyboards, fretted string instruments and saxophones produce discrete pitches. This is great intuitive preparation for the concepts of discrete vs continuous generally.
Abstract algebra
Transformational theory developed by David Lewin allows for great generality because it emphasizes transformations between musical objects, rather than the musical objects themselves.
The chromatic scale has a free and transitive action of the cyclic group , with the action being defined via transposition of notes. So the chromatic scale can be thought of as a torsor for the group .
Real and complex analysis
Real and complex analysis have also been made use of, for instance by applying the theory of the Riemann zeta function to the study of equal divisions of the octave.
Music and Mathematics as Recreational Being
Learning to play a musical instrument relies on understanding concepts, such as fractions and ratios, that are important for mathematical achievement. But the precise relation between music and math—whether musical training promotes mathematical ability, or mathematical skill influences musical ability, or whether these skills simply develop in parallel—remains unclear.

Lets look at a image how brain reacts while listening to music?
Conclusion
Our goal here was to show how music works mathematically and how the logical relations are understood in our brain, creating tranquility or tension. Obviously, we did everything using approximation (round numbers), because an analysis more accurate would be boring to the majority of the readers.
It is not necessary to memorize all that we taught in this topic; just think that music didn’t come from nowhere. Music is the result of a numeric organization. The interpretation of all these things is done by our wonderful and mysterious brain.

The final conclusion is that, if you are a musician, so in a way or another you are mathematician, because the feelings of pleasure that you feel while listening to music hide subliminal calculations. Your brain likes calculations, it is a calculating machine! The more you practice, study and know music, the more this faculty will be developed. Probably you will begin to feel pleasure while listening to songs that before didn’t bring great feelings to you.
We can compare this with a student of Physics in the first semester. If he reads a book of modern Physics, it will looks like Greek to him. It will not give him any pleasure. But some years later when he will have a good base of Mathematics and face this book again, maybe he can love the subject and could wish spend the rest of his life in this field.
REFERENCES:
- https://www.scientificamerican.com/article/is-there-a-link-between-music-and-math/
- https://musicedmasters.kent.edu/the-connection-between-music-and-mathematics/
- http://www.simplifyingtheory.com/mathematics-and-music/
- https://en.wikipedia.org/wiki/Music_and_mathematics
- https://plus.maths.org/c

For more discussion on this topic (or anything related to science), please join us on steemSTEM. SteemSTEM is a community driven project which seeks to promote well written/informative Science Technology Engineering and Mathematics postings on Steemit. More information can be found on the @steemstem blog.
ontent/magical-mathematics-music


