In obtaining the general solutions of first-order differential equations, no general formula can be used to solve them all. But however, there are some types of first-order differential equations which are a lot easier to solve than other types because it follows certain process of solution. An exact first-order differential equation is a good example. The standard form of a first-order exact differential equation is
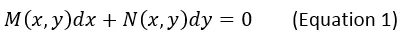Where M and N represents a polynomial expression in terms x and y. The standard form is the total differential of a reference function which can be denoted as function F (x,y). And it is derived from differentiating F like this,
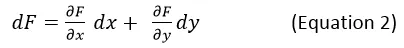Before solving for the general solution, we must first check the type of the differential equation – if it is really an exact differential equation or not. To check, the differential equation must be expressed in the standard form first. Then, we will use this equation to decide, 
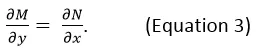Since the total differential of a reference function is equivalent to the standard form. 
Thus, from Equations 1 & 2, we can form new equations to solve for the reference function F by integration.
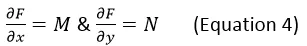The general solution is expressed in 
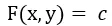(Equation 5) where “c” is an arbitrary constant. We will start on the traditional way of solving general solutions for first-order exact differential equation. Sample Problem: Obtain the general solution of
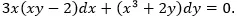
TRADITIONAL WAY ...
Step 1: Get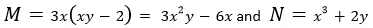
Step 2: Now, we can solve for the value of F since 
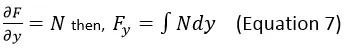Take note that M and N are equal to the partial derivatives of the reference function F with respect to x and y respectively. But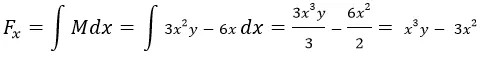
Disregard the arbitrary constant “c” on the indefinite integral. Step 3: From the equation 3, we can say that
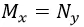
The same goes if we take a partial derivative of the reference function F with respect to “x” then, we could say that it is equal to the sum of the partial derivative of F_y with respect to x and an unknown component which can be denoted as T’(x) which contains variable “x” only. 
Going back to our solution, we will solve for the value of T(y).
Since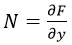 
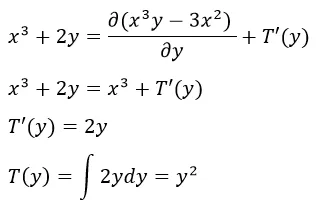
Disregard the arbitrary constant “c” here. Thus,
SHORTHAND WAY ...
Using these formula, you can solve the general solution of first-order exact differential equations directly.
Or you can also use
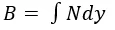With the same sample problem, let us solve for the general solution using Equation 9.
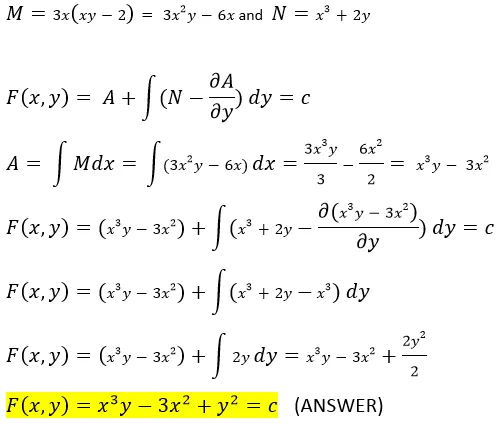To check for accuracy of our shorthand method and for comparison, we will use Equation 10, and let’s see if we will have the same answer this time.
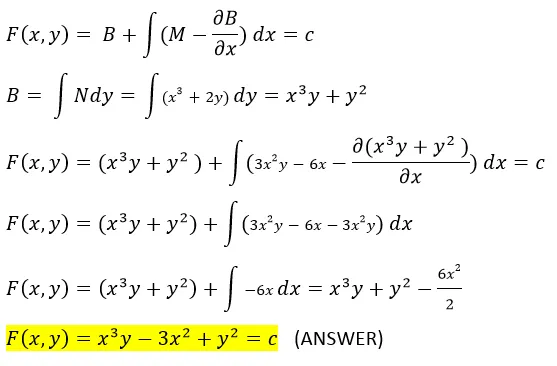Using Equation 9 and 10 to obtain the general solution of the first-order exact differential equation yield us the same correct answers when we solve it using the traditional way.
The shorthand method just follows the necessary procedure done on the traditional method using less variables and steps. I personally created this method when I was on my 3rd year in College while taking up Differential Equations. It had saved me some time during examinations especially when there are a lot of items to solve. Moreover, using this method, I have also the extra time to check for my answers. However, this method is only applicable to first-order exact differential equations.
HOW DID I COME UP WITH THESE FORMULA?
The shorthand way in obtaining the general solution of first-order exact differential equation is derived from traditional method on the above solution. It eliminates the use of several steps and variables. On the step 3 of the traditional method, you can observe that the use of variable T'(y) can be eliminated if you replace it with
PROS and CONS
This is useful when there are a lot of problems involving the same type of differential equations but I would recommend that the traditional method must be used when it is not necessary to be in a hurry. Understanding the concepts is better than memorizing a shorthand formula. Morever, some professors may not like shortcuts so you should use this when solutions are not necessary.Reference: Rainville, E. D., Bedient, P. E., & Bedient, R. E. (1997). Elementary differential equations. Upper Saddle River, NJ: Prentice Hall.
Image Credits: https://steemit.com/steemstem/@foundation/steemstem-promotional-sticker-fund-raiser
"Support the steemSTEM community by following @steemstem."
Learn with us on Discord.
“That’s all. ‘Til next time. I hope you learn something useful today.”