Everybody is familiar with the six-sided die with values from one to six on its faces, but what would happen if we start mixing it up a bit? If we play with the numbers, we can come up with all kinds of interesting configurations. if we start altering the faces, there will be some variations that are going to be stronger than others and would give us a better chance of winning if we play one on one against a different dice.

The Simplest of Examples
For instance, if we adjust all six sides of a die to show 6, this would beat a regular die or a die that has only fives on each side. This means we can take a pair of dice and determine if one is stronger than the other. While the dice with the same number on all sides are pretty simple, we could have options that are a bit more groovy like the example below.

Still, there is a very clear winner. As any number on the red die can beat any number from the green die, we can say that the red die is not only stronger, but also has 100% probability of winning. The red die is going to win every single game against the green one.
But let's look into some cases that are a bit more curios where the probabilities are not so simple and the outcome is not always that straightforward.
The More Interesting Case

Let's try to determine which of one of the three dice above is the strongest one. Many people's first instinct might be to calculate the average score each die can get you and go from there. But if we try that we'll notice that the sum of the six sides from each of the dice above is 21 giving all of them an average score of 3.5.
Well if this approach doesn't work, let's try to examine pairs and try to see how each die fares against the others.
Yellow vs. Blue
To determine which of the two is stronger, we actually have to examine each outcome's probability. Let's try to do that avoiding complicated math first. The yellow die can roll two different numbers. If it rolls a 3, the blue die has 50% chance of winning because half of its faces are higher while the other half of its faces are lower than 3. So if the yellow die rolls a 3, both dice have an equal chance of winning depending on what the blue die rolls. But if the yellow die rolls a 6, the blue die has no chance of winning and while the yellow die will roll a 6 less often, it still gives it an edge.
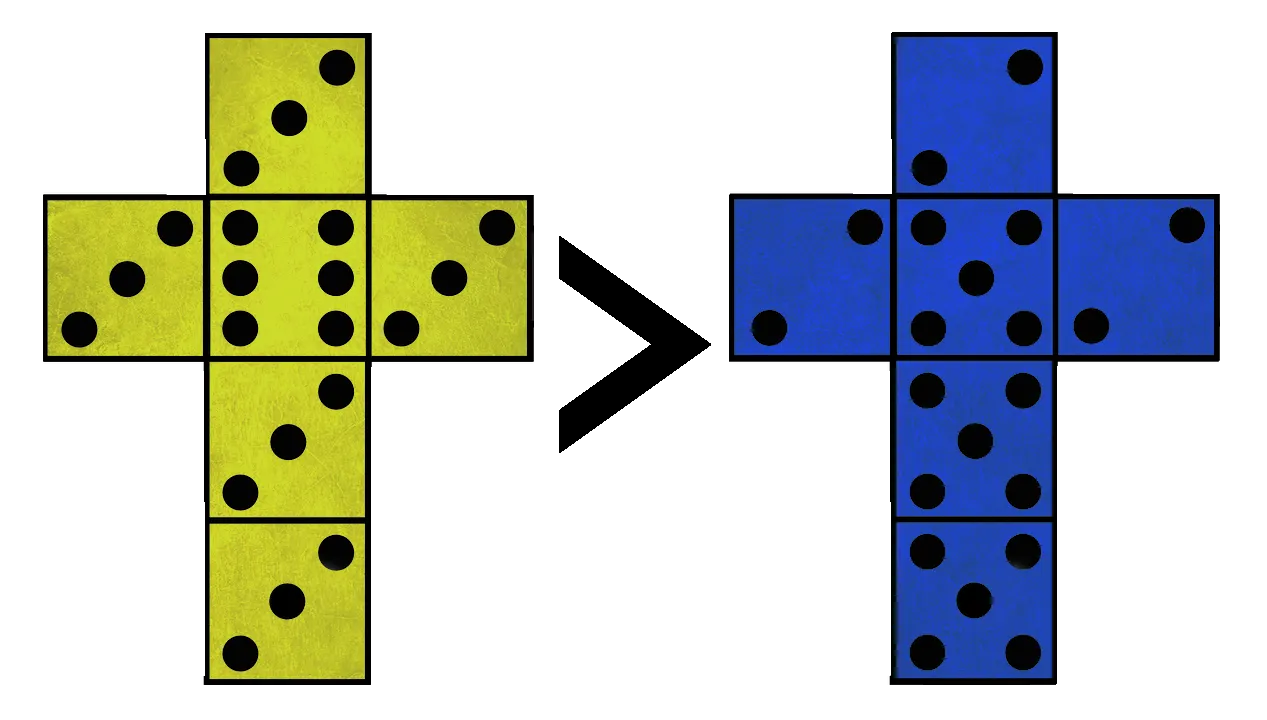
Of course, we can also calculate the exact probabilities. The yellow die will roll a 3 with probability of 5/6 and since the blue die can roll either a 2 or a 5 with a probability of 1/2, either outcome gets a probability of 5/12. The probability of the yellow die rolling a 6 is 1/6 and that's also the probability of it winning in that case. So the total probability of the blue die winning is 5/12 and the total probability of the yellow die winning is 5/12 + 1/6 which is 7/12. This is 58.3%.
Blue vs. Purple
When we compare the blue die and the purple die, we can do very similar analysis. If the purple die rolls 4, it is going to have 50% chance of winning as half of the blue die's faces are higher and the other half are lower. But if the purple die rolls 1, it is going to loose to the blue one no matter what as all of the blue die's faces are higher. The math works out in the exact same way with the probability of the blue die winning being 7/12 while the purple die has to settle with only 5/12.

But does this mean that the yellow die is the strongest and the purple die is the weakest in this selection? Let's check!
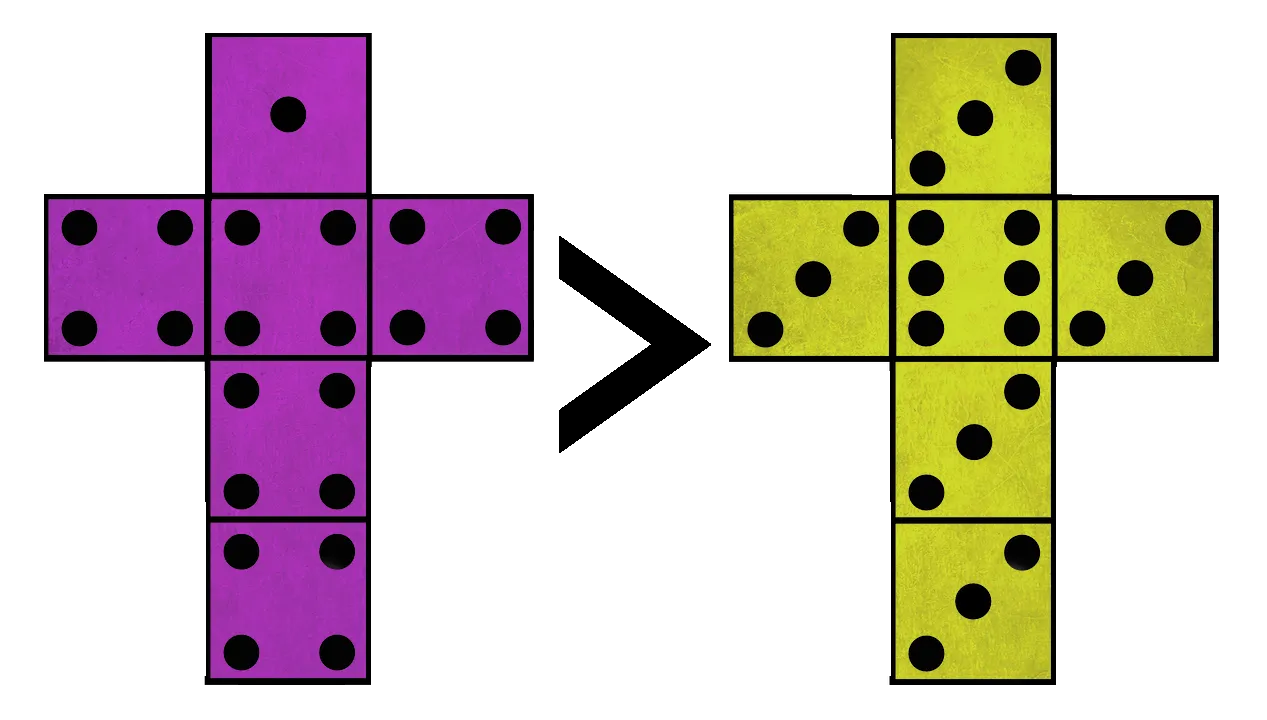
Purple vs. Yellow
If you look carefully at the two configurations, it's actually quite easy to see that the purple die is stronger even without doing the math. If the purple die rolls 1 it loses automatically, but the purple die has only one such side. The probability of losing in this case is just 1/6. But if the purple die rolls 4, it faces very good chances as the yellow has only one face that could beat it giving it a chance of 5/6. And since the chance of rolling a 4 is 5/6, too, we multiply the two probabilities to get the total probability of the purple die beating the yellow die which is 25/36. Turns out that the purple die is not only not the weakest but it has a 69.4% chance of beating the yellow one which we thought might be the strongest.
So which die is objectively the strongest from the bunch?

Well, apparently none. In this group of dice there is no die that is the strongest while each pair produces an advantage for one of the dies. If you have those 3 dice and you want to play against a friend, you can always graciously give them the advantage of examining the dice and choosing first. This will make your chances of victory higher because you can always choose a die that will beat their chosen one. Of course, since the probabilities are never 100%, you are not guaranteed to win, especially in a shorter game, but the odds will be significantly tilted in your favor. Remember, casinos make a killing with much smaller advantages.
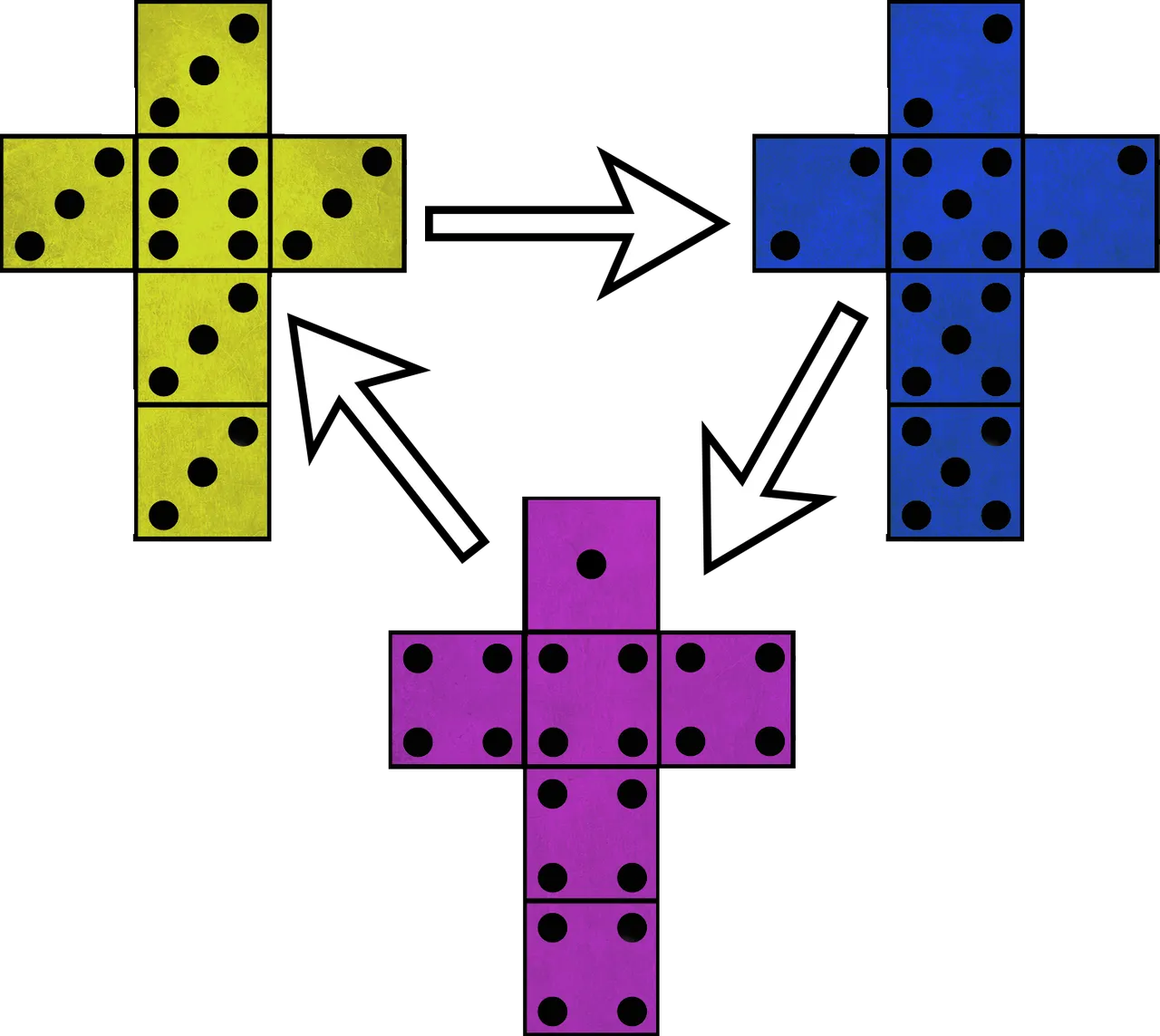
Such groups of dice are called non-transitive dice and their strength works in a circle just like a game of rock/paper/scissors. There are other such combinations of dice that exhibit similar properties where a group of dice doesn't have a clear favorite, but the pairs of likely winners and losers and arranged in a circle.
The Moral of the Story
It's important to know about this effect when dealing with probabilities because our intuition about that could easily mislead us. The fact that A is more probable than B in a head to head comparison and B is more probable than C in another head to head comparison by no means proves that A is more probable than C. It sounds like a very logical conclusion, but it is not a conclusion that one could draw with any level of certainty. In many cases A would in fact be more probable than C, but not always. Sometimes reality is going to go against our intuition and C would actually be more probable than A just like it is with non-transitive dice.
Knowing this is possible is very important when trying to interpret data that comes from more than one source as the different head to head comparisons we might be looking at might still be hiding the full picture from us. Before a conclusion can be drawn with certainty, the relation the we are claiming needs to be tested itself, not just inferred circumstantially from other relations.
I hope you found this interesting and I hope it will be yet another reason for you to always question your intuition, instead of jumping to conclusions. Our innate human intuition did not evolve to calculate probabilities correctly or to deal with large sets of data, so we should try to always check it instead of relying on it.

Sources:
- James Grime 2010 | http://singingbanana.com/dice/article.htm
- https://en.wikipedia.org/wiki/Nontransitive_dice
All images are original unless a specific source is cited.
