Hola de nuevo estimados amigos de #stem-espanol.
En esta oportunidad, les presentaré una modificación al modelo Oscilador Armónico que estudiamos en el post anterior. Esta modificación fue postulada por Terry Fred Jr., científico del Laboratorio de Electrónica del Estado Sólido de la Universidad de Michigan (EE UU), para ajustar la función dieléctrica compleja de los cristales AlxGa1-xAs (Ref 1). Por otro lado, estaremos describiendo la naturaleza de la función dieléctrica compleja.

Presentación de física en STEM-espanol. Explicación al final del post.
En el anterior post (ver aquí) aprendimos sobre las relaciones de dispersión óptica en cristales semiconductores. Así mismo, se mostró un ajuste Lorentziano sobre la gráfica de la constante dieléctrica imaginaria, en función de la energía de la luz incidente, en el semiconductor CdTe, la cual fue descrita en un previo post (ver aquí).
En resumen, las relaciones de dispersión denotan los valores de energía de la estructura de bandas de un cristal semiconductor mediante el uso de los fenómenos ópticos. En otras palabras, estas relaciones de dispersión describen las transiciones energéticas de los electrones desde la banda de valencia hasta la banda de conducción por la absorción de fotones energéticos.
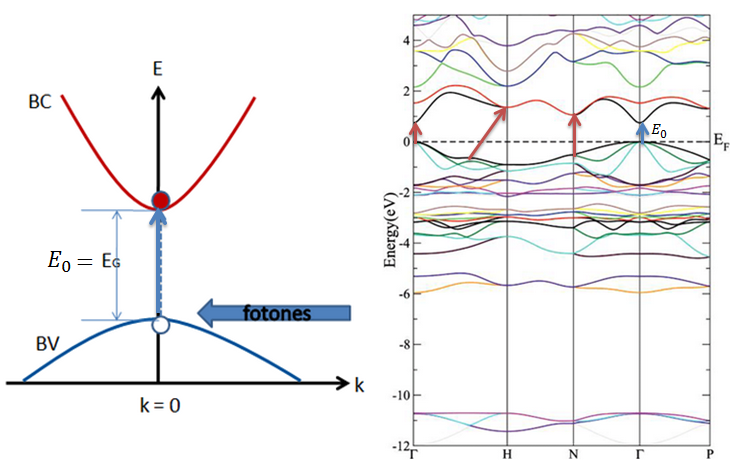
Figura 1. Estructura de bandas, transición fundamental
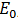 y posibles transiciones de bandas/relaciones de dispersión. Fuente: @iamphyisical (aquí)[https://steemit.com/stem-espanol/@iamphysical/como-determinar-la-brecha-de-energia-en-un-semiconductor], Edición: @djredimi2.
y posibles transiciones de bandas/relaciones de dispersión. Fuente: @iamphyisical (aquí)[https://steemit.com/stem-espanol/@iamphysical/como-determinar-la-brecha-de-energia-en-un-semiconductor], Edición: @djredimi2.La estructura de bandas entonces es una versión amplificada de la transición fundamental banda a banda, y las relaciones de dispersión representan los valores de la energía para la transición electrónica. En este caso la energía fundamental (es decir el mínimo valor de energía) es igual a la brecha de energía del cristal estudiado.
LA FUNCIÓN DIELÉCTRICA
Para explicar la definición de un dieléctrico es necesario estudiar el movimiento de las cargas en el interior de un material. Para que las cargas eléctricas internas de un material se muevan es necesario la excitación de su estado de equilibrio mediante interacciones o fuerzas externas. Si aplica un campo eléctrico sobre un material específico, transcurrido un tiempo se alcanzara el equilibro electrostático. Dependiendo de este tiempo, las cargas internas pueden ordenarse, describiendo al material como buenos conductores o dieléctricos. A este ordenamiento se le conoce como Polarización.
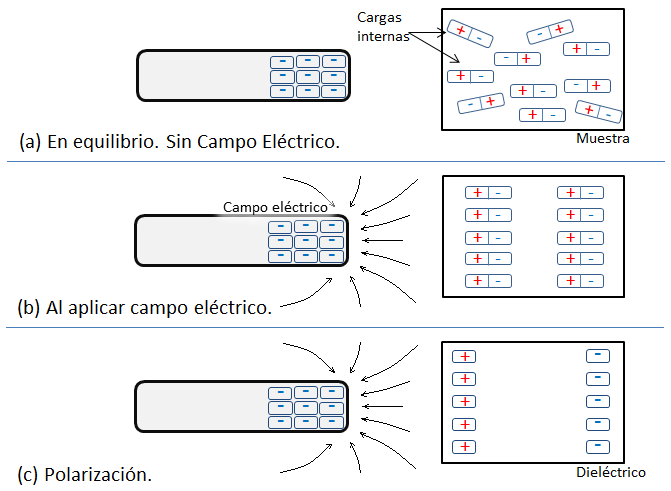
Figura 2. Ordenamiento de cargas internas por efecto de un campo eléctrico externo. Autor: Lic. Daiver Juarez, @djredimi2 con la ayuda de Microsoft Power Point.
Este movimiento de cargas internas se describe comúnmente con un campo eléctrico estático que resulta en una constante dieléctrica real. Sin embargo, el desplazamiento de estas cargas no puede seguir instantáneamente al campo eléctrico. Esto se debe a efectos inerciales de las cargas, lo que implica un desfase entre el campo eléctrico y la respuesta del sistema. Es por este desfase que se describe a la constante dieléctrica como una función compleja, y se conoce como:
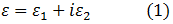
Donde 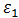
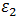
En cristales semiconductores las cargas internas que se mueven son los electrones y los huecos. Estos se trasladan desde la banda de valencia hasta la banda de conducción debido a la absorción de fotones energéticos.
Mediante el uso de técnicas experimentales como la Elipsometría Espectroscópica podemos determinar las constantes dieléctricas. Esto se logra gracias a que la Elipsometría mide el cambio en estado de polarización de la medida del haz inducido y el haz por la reflexión de la muestra. En otras palabras, el estado inicial de la muestra es afectado por la energía de la luz polarizada, provocando el movimiento de las cargas internas (En este caso la luz polarizada incidente actúa como el campo eléctrico). De esta manera, el haz de luz reflejado muestra las propiedades de dicha muestra de estudio.
FUNCIÓN DIELÉCTRICA PARA UN SISTEMA RESONANTE.
Las transiciones energéticas de banda a banda pueden describirse mediante un modelo de absorción resonante en un oscilador armónico forzado. Debido a que estamos aplicando una fuerza externa que varía armónicamente con el tiempo, la fuerza total que actúa sobre este sistema es igual a la suma de la fuerza recuperadora lineal, la fuerza de amortiguamiento y la fuerza impulsora:
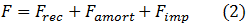
Para una partícula del sistema de masa 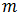
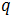
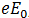
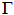
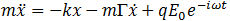
Por definición 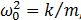
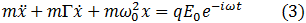
Empleando una solución armónica para el desplazamiento de dicha partícula, es decir, 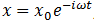
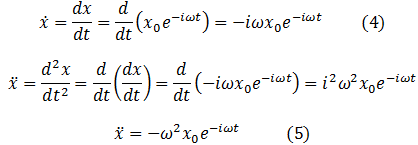
Sustituyendo estos valores en (3), nos queda:
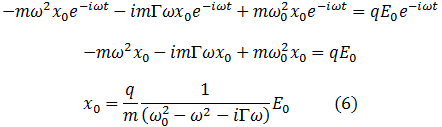
Donde 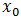
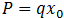
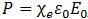
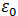
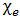
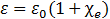
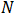
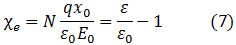
Sustituyendo la ecuación (6) en (7), y despejando ε
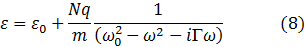
Esta ecuación representa la función dieléctrica compleja.
Demostración del cálculo de ε1 y ε2.
Multiplicando y dividendo por el inverso aditivo del denominador para reagrupar los términos reales y complejos.
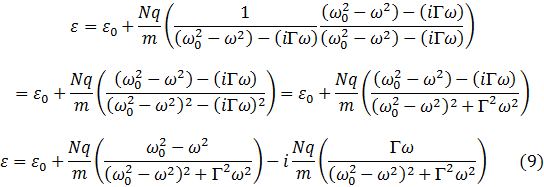
Comparando con la ecuación (1),
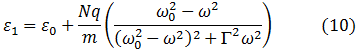
Y,
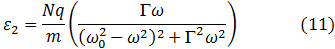
Si representamos 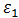
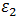
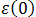
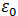
Para ε1. y = y0 + (A*((x^2-xc^2)/((x^2-xc^2)^2 + (w*x)^2)))
Para ε2. y = (A*(w*x/((x^2-xc^2)^2 + (w*x)^2)))
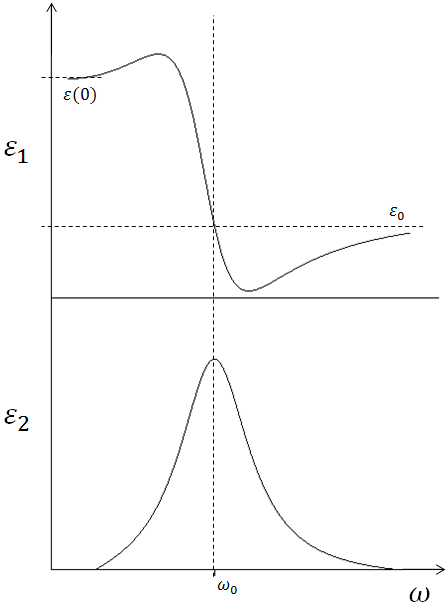
Figura 3. Constante dieléctrica real e imaginaria de un sistema resonante según ecuaciones (10) y (11). Autor: Lic. Daiver Juarez, @djredimi2 con la ayuda del software OriginPro 8.
El modelo Lorentziano presentado en el post anterior (ver aquí) es equivalente a la constante dieléctrica compleja mostrada en la ecuación (11) relacionando la frecuencia de las oscilaciones resonantes con la energía de los fotones. De esta manera el modelo Lorentziano viene a ser de vital importancia para el cálculo de la estructura de bandas.
Cualquier modificación a la función dieléctrica (ecuación (8) y (9)) resulta debido a la inclusión de fuerzas de interacción con el sistema, así como también para que el modelo se ajuste con mayor eficiencia a los datos experimentales.
LA MODIFICACIÓN DE LA FUNCIÓN DIELÉCTRICA COMPLEJA.
La propuesta de Terry Fred Jr. resulta de una modificación a la función dieléctrica compleja (basada en la función Lorenziana). En ella se considera que 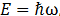
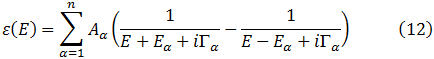
Donde 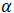
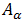
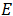
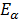
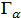
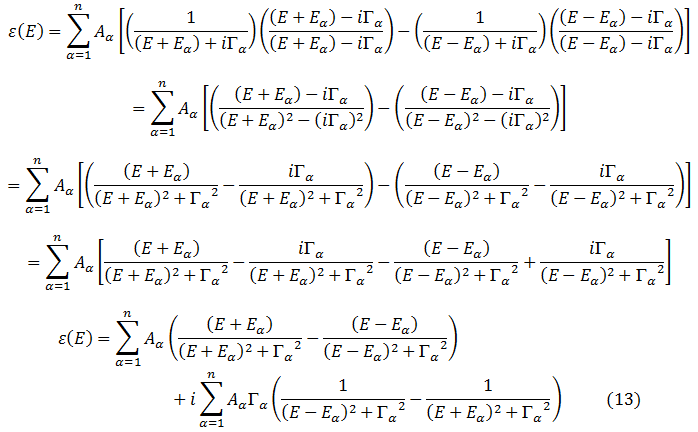
Por último comparando con la ecuación (1),
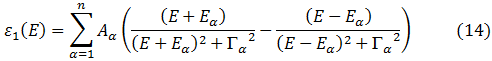
Y
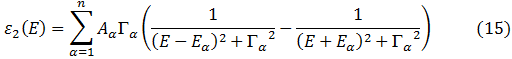
Con la ayuda del Software matemático Originpro 8 (ref 3) se muestra la gráfica (figura 4) de las ecuaciones (13) y (14), donde alfa=1. Estas gráficas denotan las mismas gráficas de la figura 3, por lo que se considera una aproximación aceptable. La ecuaciones usadas para graficar en el software origin son:
Para ε1(E). y = (A*((x+xc)/((x+xc)^2 + (w^2)))) - (A*((x-xc)/((x-xc)^2 + (w^2))))
Para ε2(E). y = (A*(w/((x-xc)^2 + (w^2)))) - (A*(w/((x+xc)^2 + (w^2))))
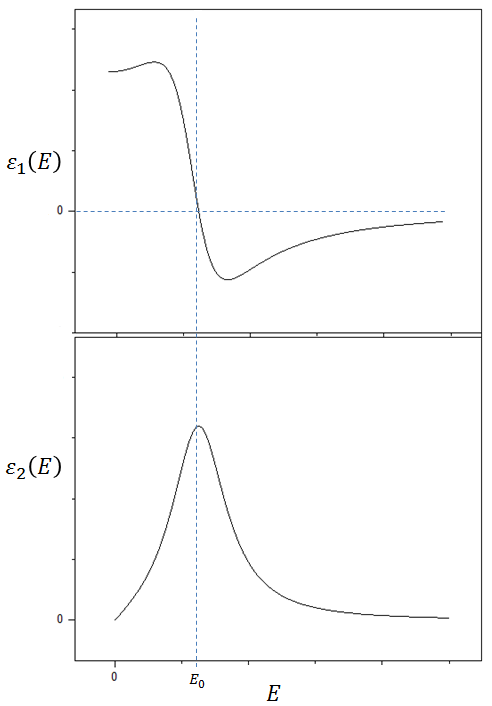
Figura 4. Constante dieléctrica real e imaginaria de un sistema resonante según ecuaciones (14) y (15). Autor: Lic. Daiver Juarez, @djredimi2 con la ayuda del software OriginPro 8.
En el próximo post les quiero mostrar el ajuste experimental sobre la función dieléctrica de cristales semiconductores mediante el análisis multi-picos del software Origin. Hasta la próxima amigos.
POST DE INTERÉS.
- Por @djredimi2 - FÍSICA DEL ESTADO SÓLIDO: Introducción a los Semiconductores. .
- Por @iamphysical - ¿Cómo determinar la brecha de energía en un semiconductor?.
- Por @djredimi2 - ELIPSOMETRÍA ESPECTROSCÓPICA (SE). Propiedades ópticas del semiconductor CdTe.
- Por @djredimi2 - Determinación de las relaciones de Dispersión Óptica de cristales Semiconductores. Ajuste Lorentziano..
REFERENCIAS BIBLIOGRÁFICAS.
(1) Fred L. Terry Jr. (1991). "A modified harmonic oscillator approximation scheme for the dielectric constants
of AlxGa1−xAs. University of Michigan, EEUU. Solid State Electronics Laboratory, Department
of Electrical Engineering and Computer Science. Journal of Applied Physics 70, 409.
(2) Universitat de Valencia. "Lección 9. Propiedades ópticas de los semiconductores". [Documento en linea].
(3) OriginLab Corporation. (2007). "Origin 8 User Guide". First Edition. Northampton, USA. [Documento en linea].
En #stem-espanol, el grupo día a día trabaja arduamente por avanzar en el servicio y el apoyo a la comunidad de Steem que publica sobre Ciencia, Tecnología, Ingeniería y Matematicas (STEM) en nuestro idioma español. Es por eso, que se han abiertos "sub-grupos" de #stem-espanol relacionados a temas específicos de STEM. Resultando en el nacimiento de FÍSICA en #stem-espanol (imagen previa) (Aquí el post informativo). Es gracias a esta gran noticia, que se ha preparado un equipo organizador para coordinar las actividades relacionadas a la comunidad y al sub-grupo.

Si estas interesado en Física, te invito cordialmente a unirte al sub-grupo #fisica del chat de stem-espanol, registrandote en discordapp.com y accediendo a este enlace. Por último, puedes postear publicando bajo la 3era etiqueta #stem-fisica. La 1era y la 2da etiqueta deben ser #stem-espanol y #steemstem respectivamente.
Para saber más sobre stem-espanol visita en Steem al canal principal @stem-espanol y al canal general @steemstem.