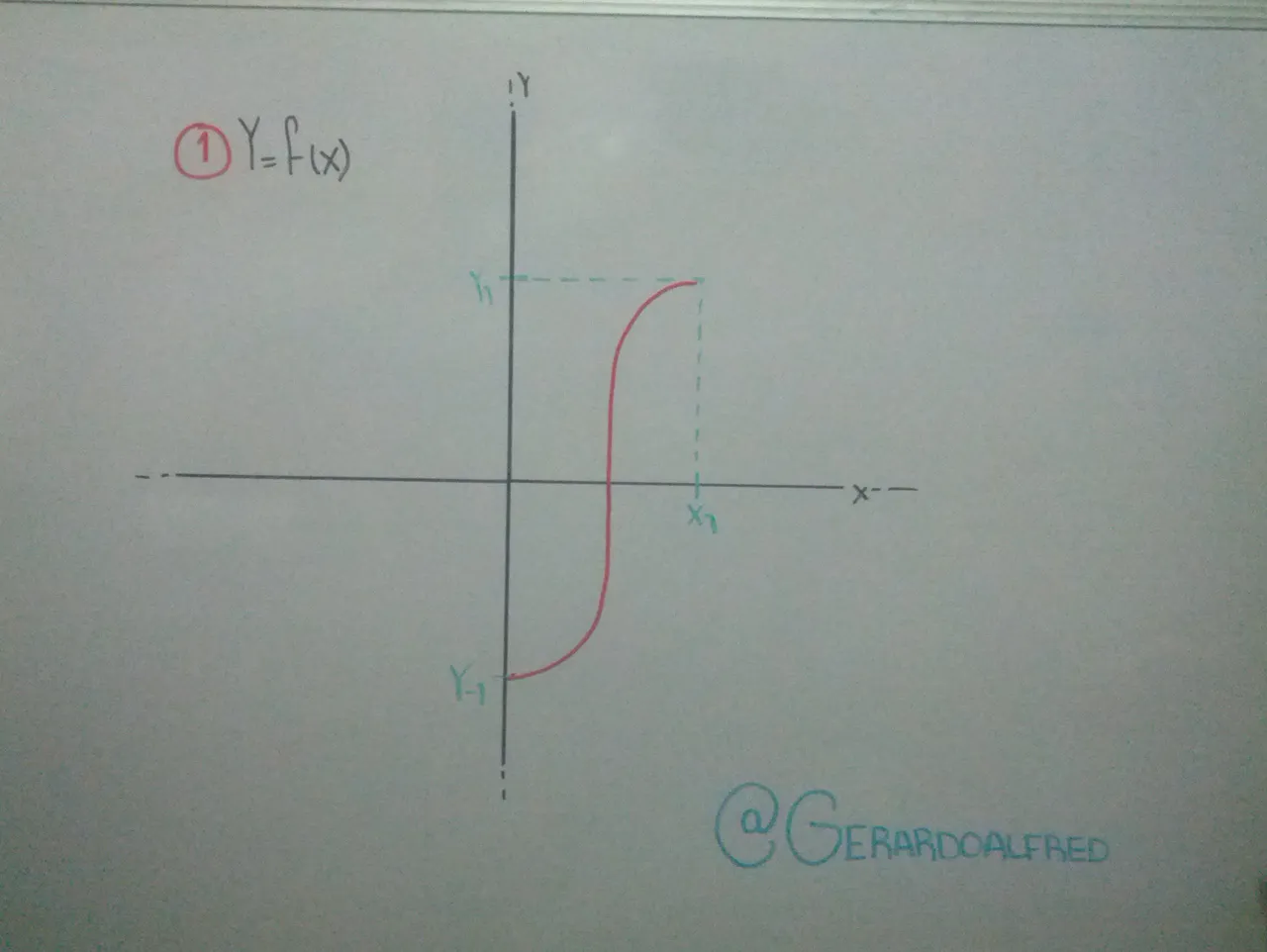
¿Qué es una función?
Es un trazo de curva que cumple una trayectoria, siempre y cuando satisfaga la siguiente condición: para cada valor de "x" existe una "y" solo una imagen en "y"
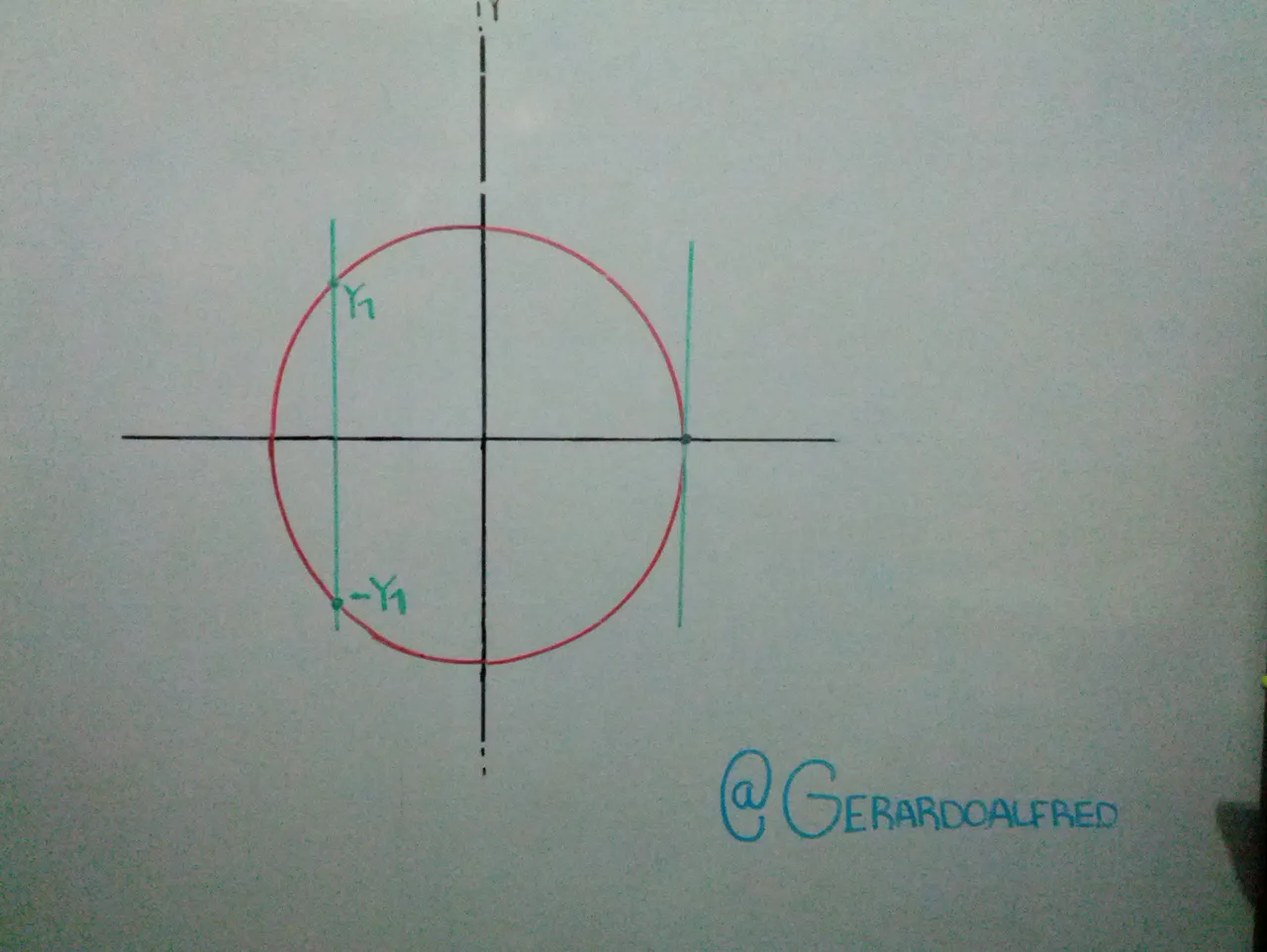
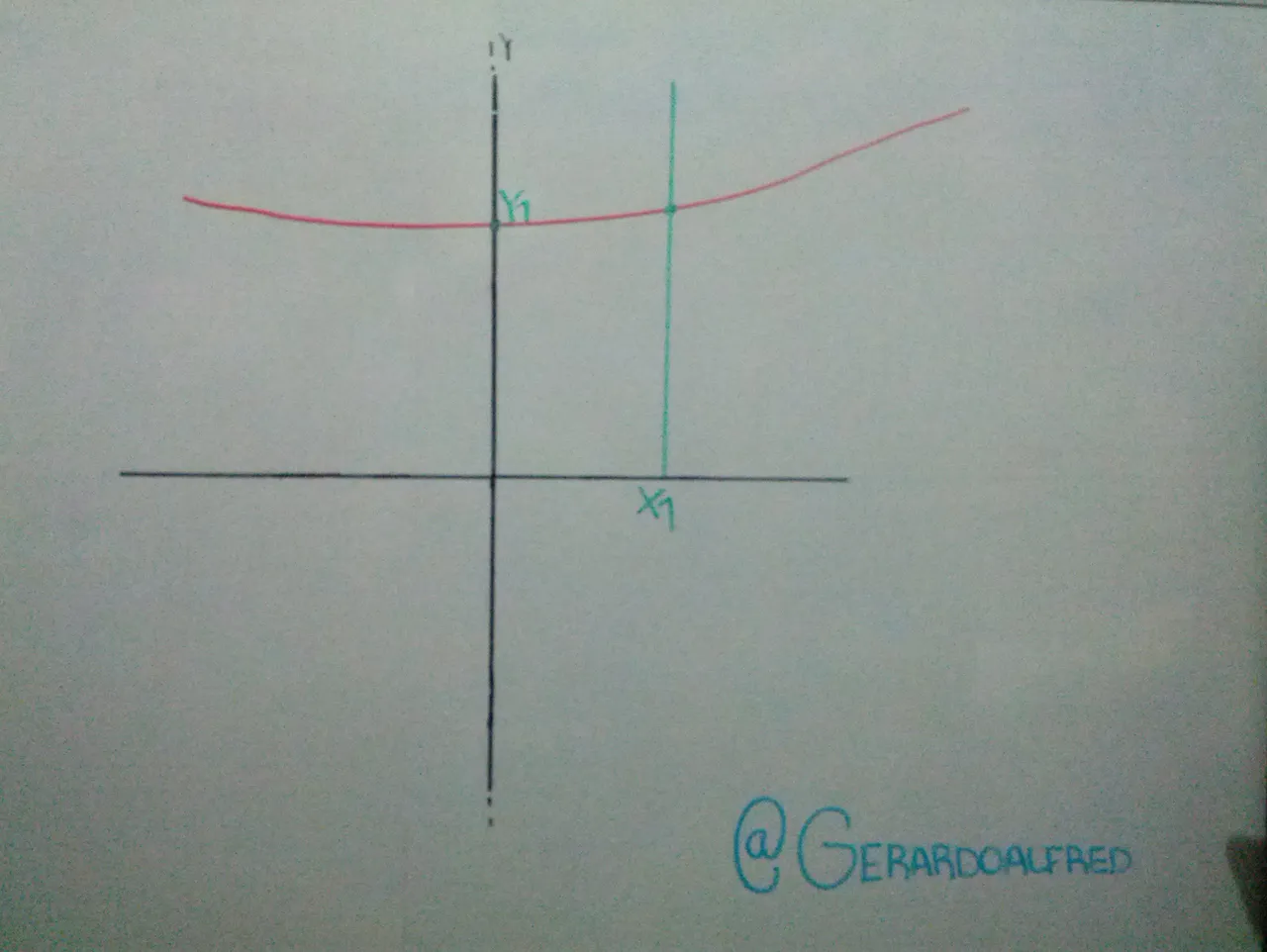
Función generalizada
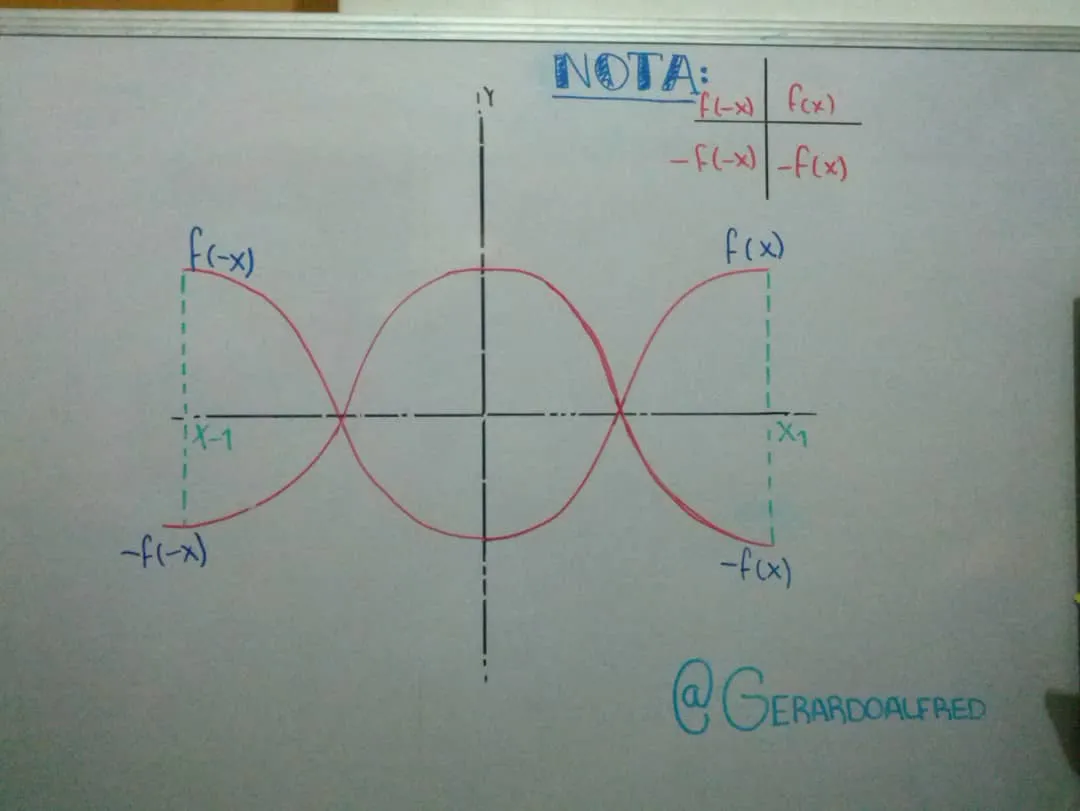
En la imagen se puede observar varias funciones generalizada en todos los cuadrante del eje de coordenadas, conociendo el gráfico de una función y=F(x) podemos obtener, mediante simples transformaciones geométricas los siguientes gráficos de las funciones
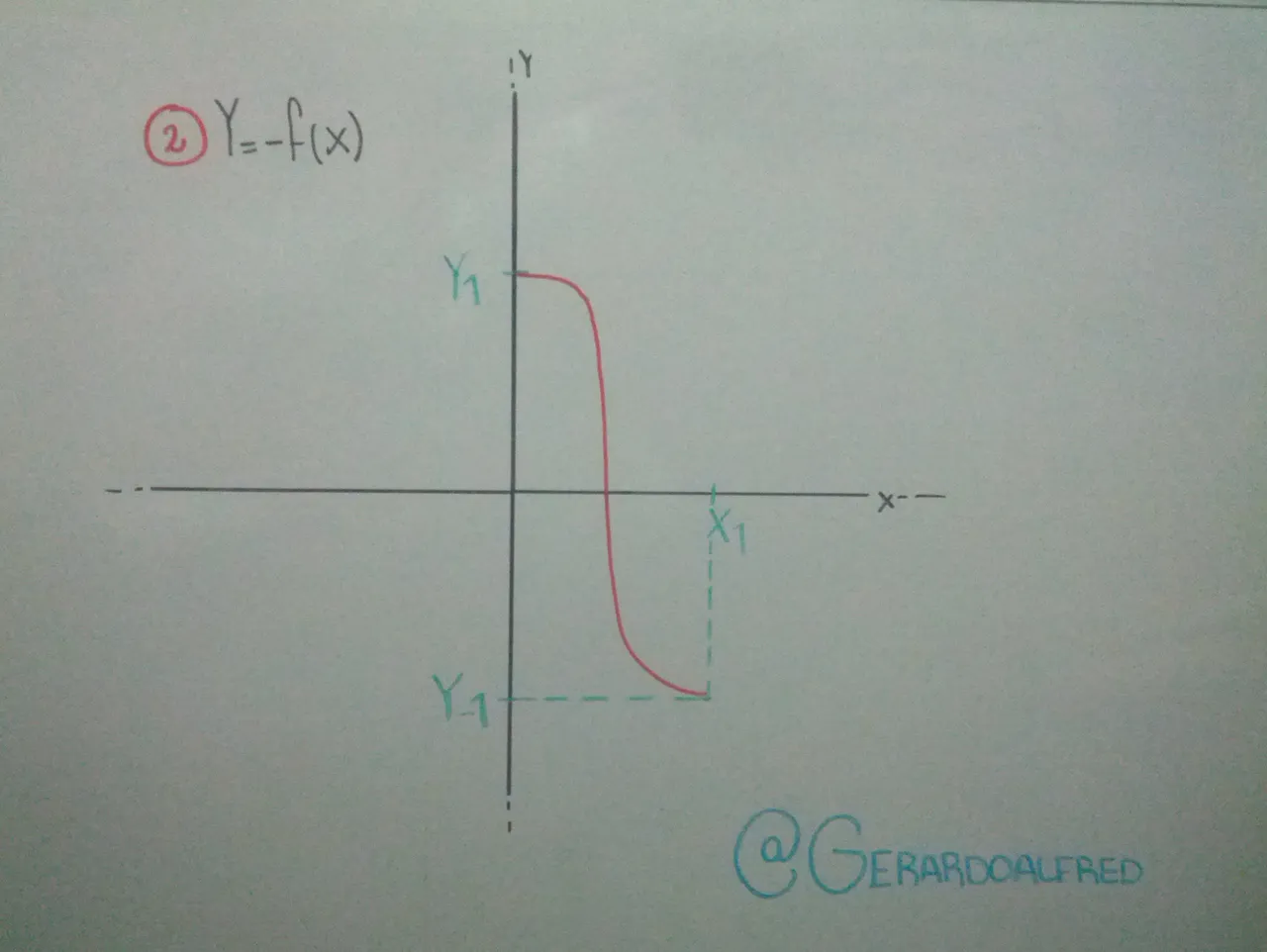
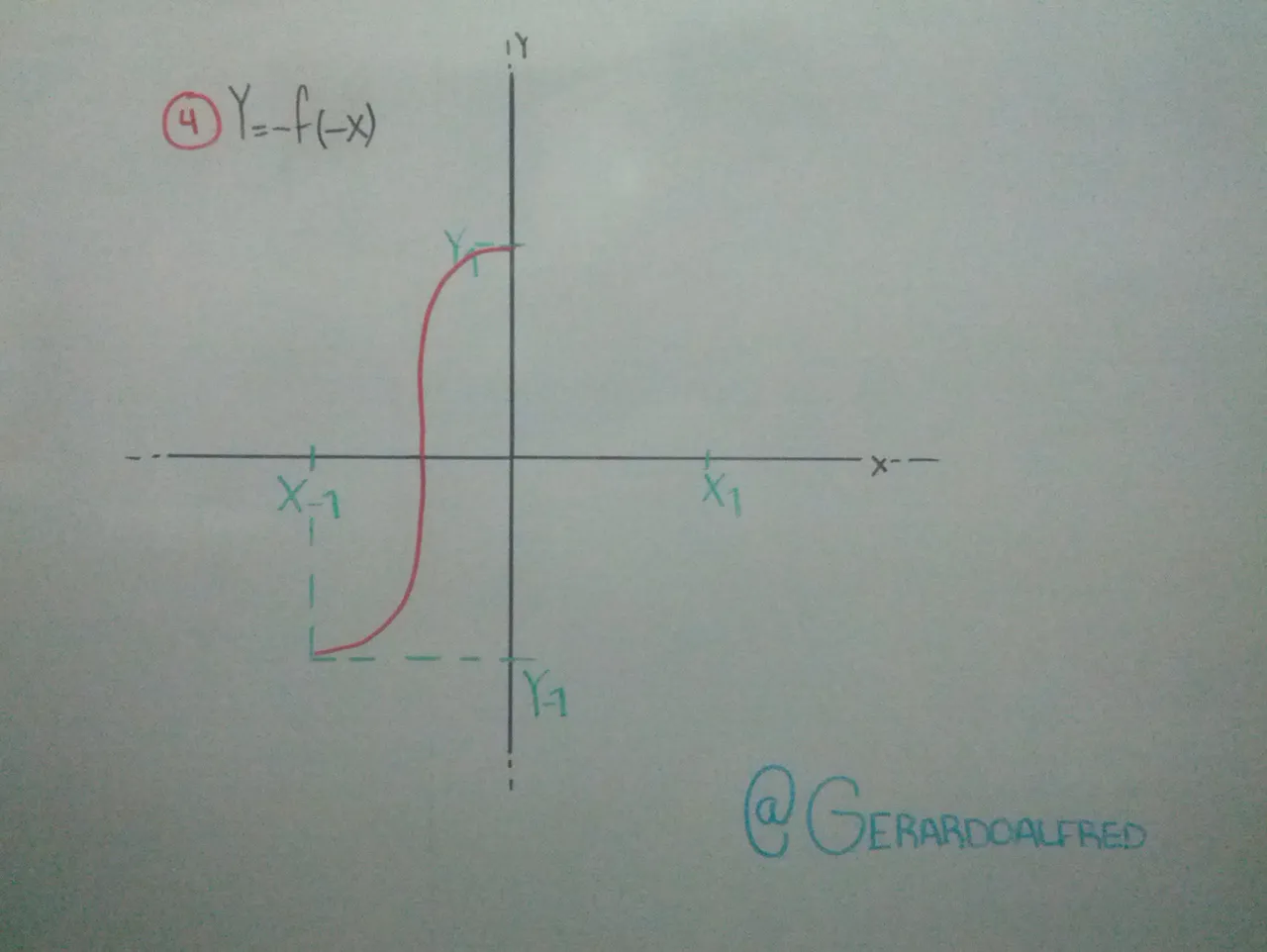
Cuando el menos esta afuera -F(x), esto quiere decir que la función F(x) se voltea con respecto al eje x (haciendo referencia a la imagen número 2).
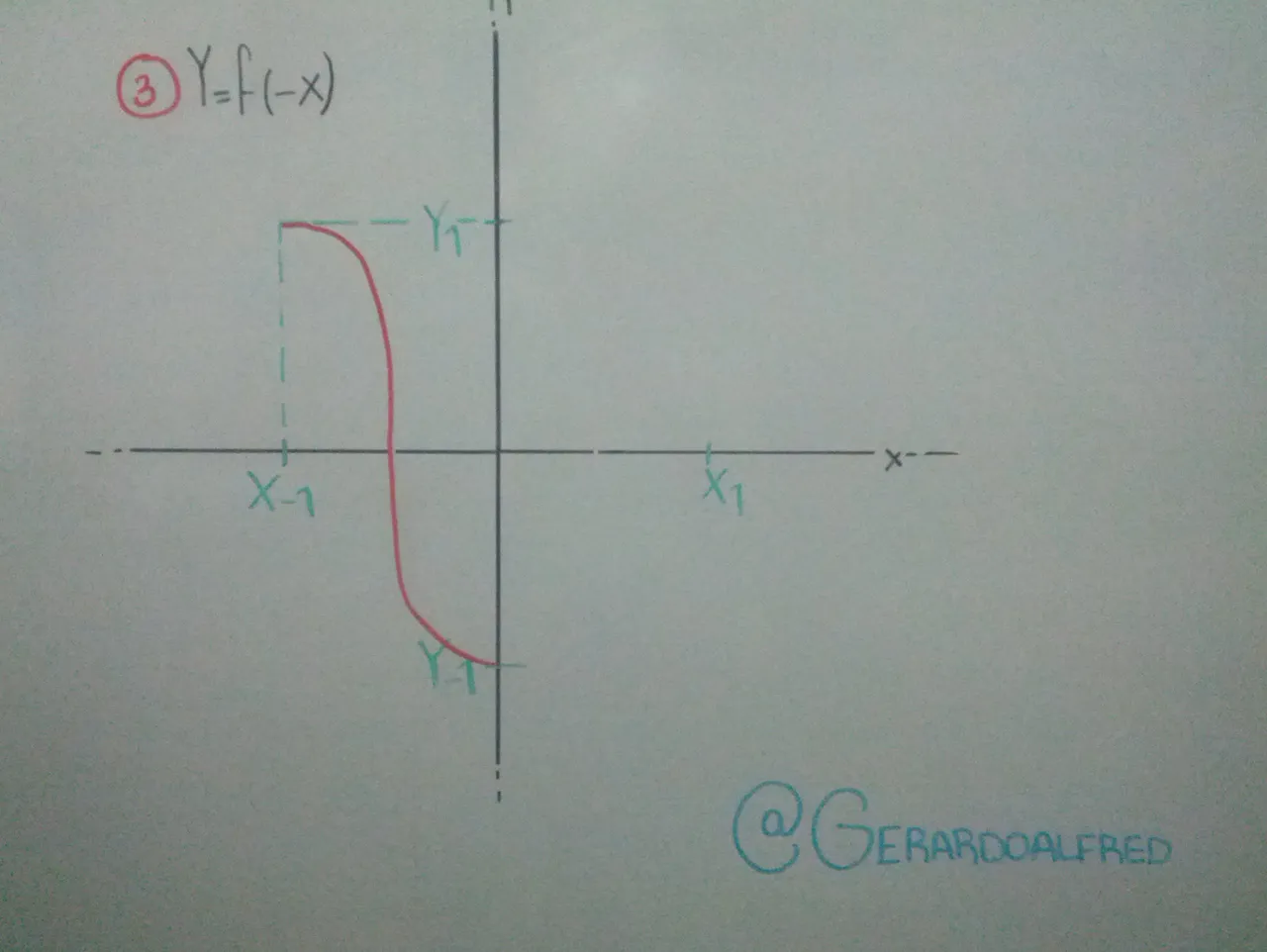
Cuando el menos esta dentro del argumento F(-x), esto quiere decir que la función original F(x) se voltea con respecto al eje "Y" ( haciendo referencia a la imagen número 3).
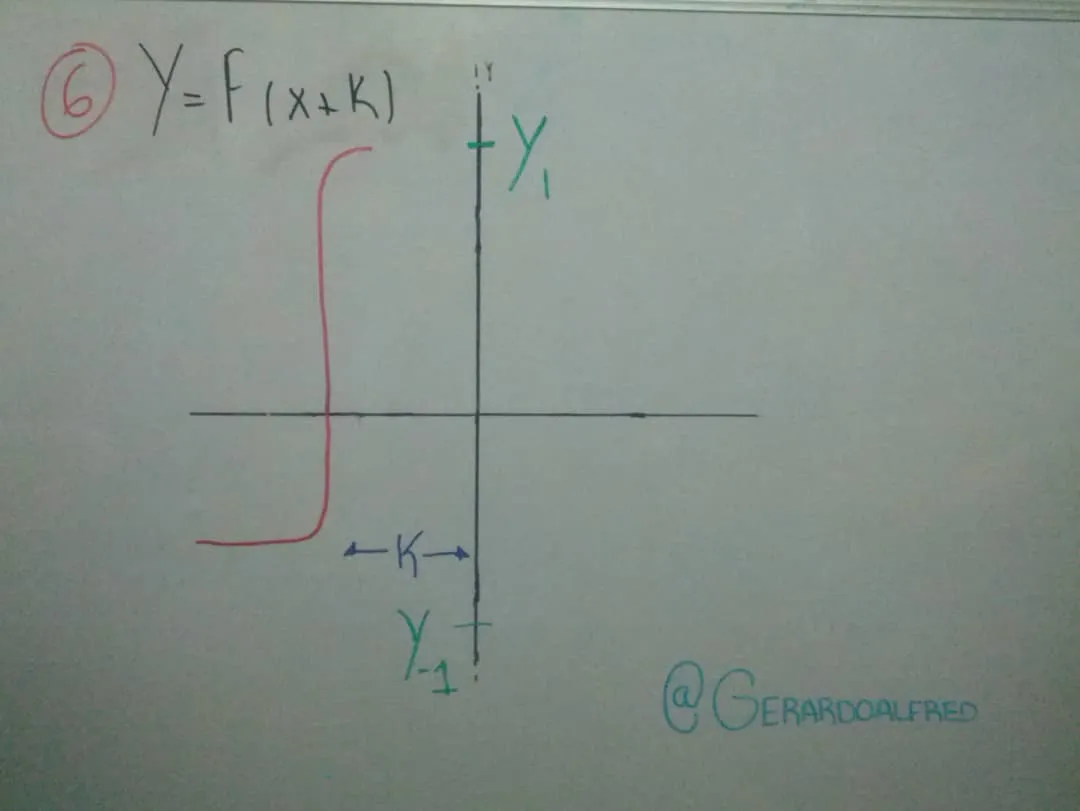
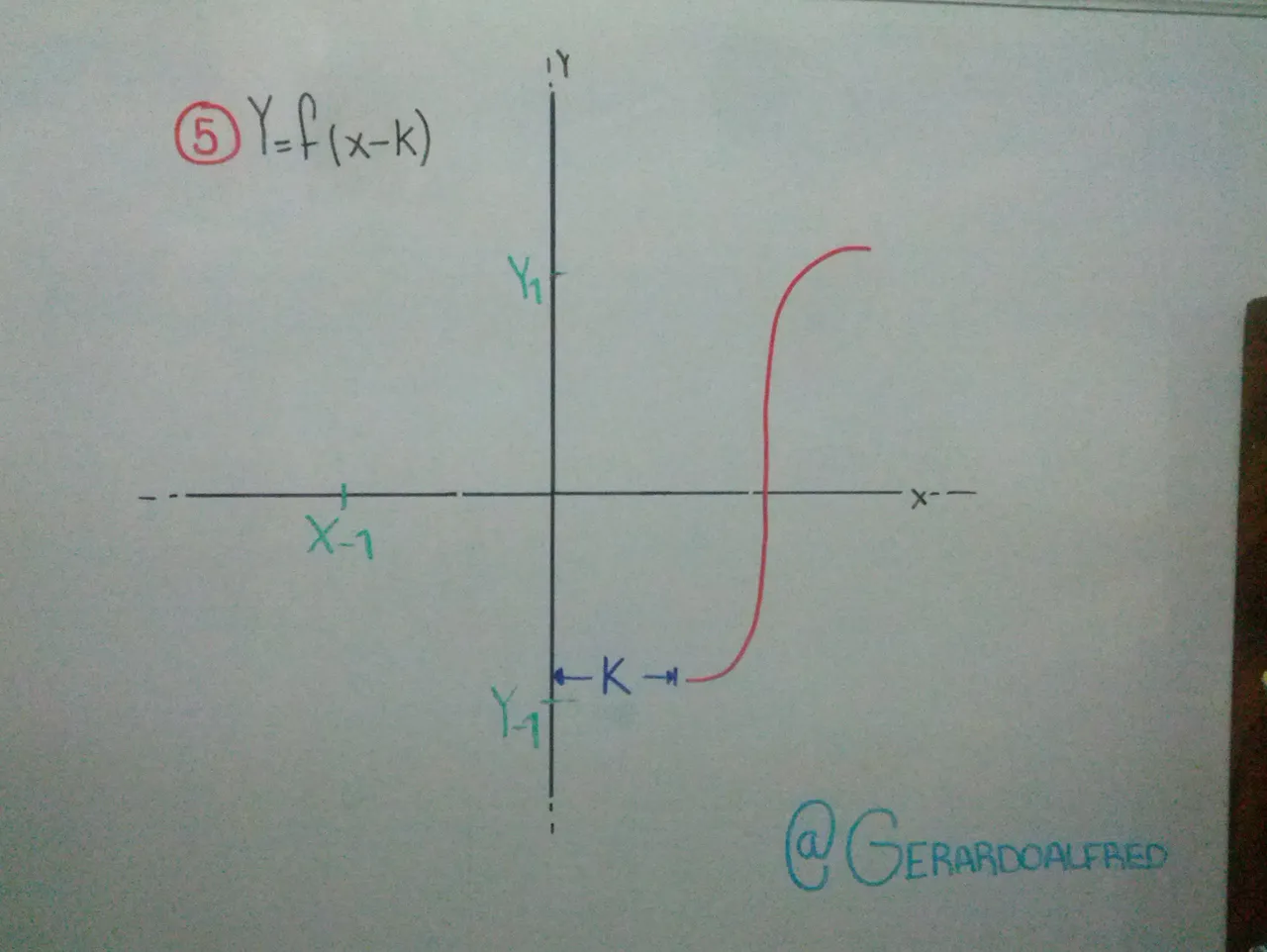
Cuando tenga un valor K dentro del argumento , F(x ± K ), esto quiere decir que la función se traslada por sobre eje x , si el valor de K es negativo se traslada a la derecha y viceversa (haciendo referencia en las imágenes 5 y 6).
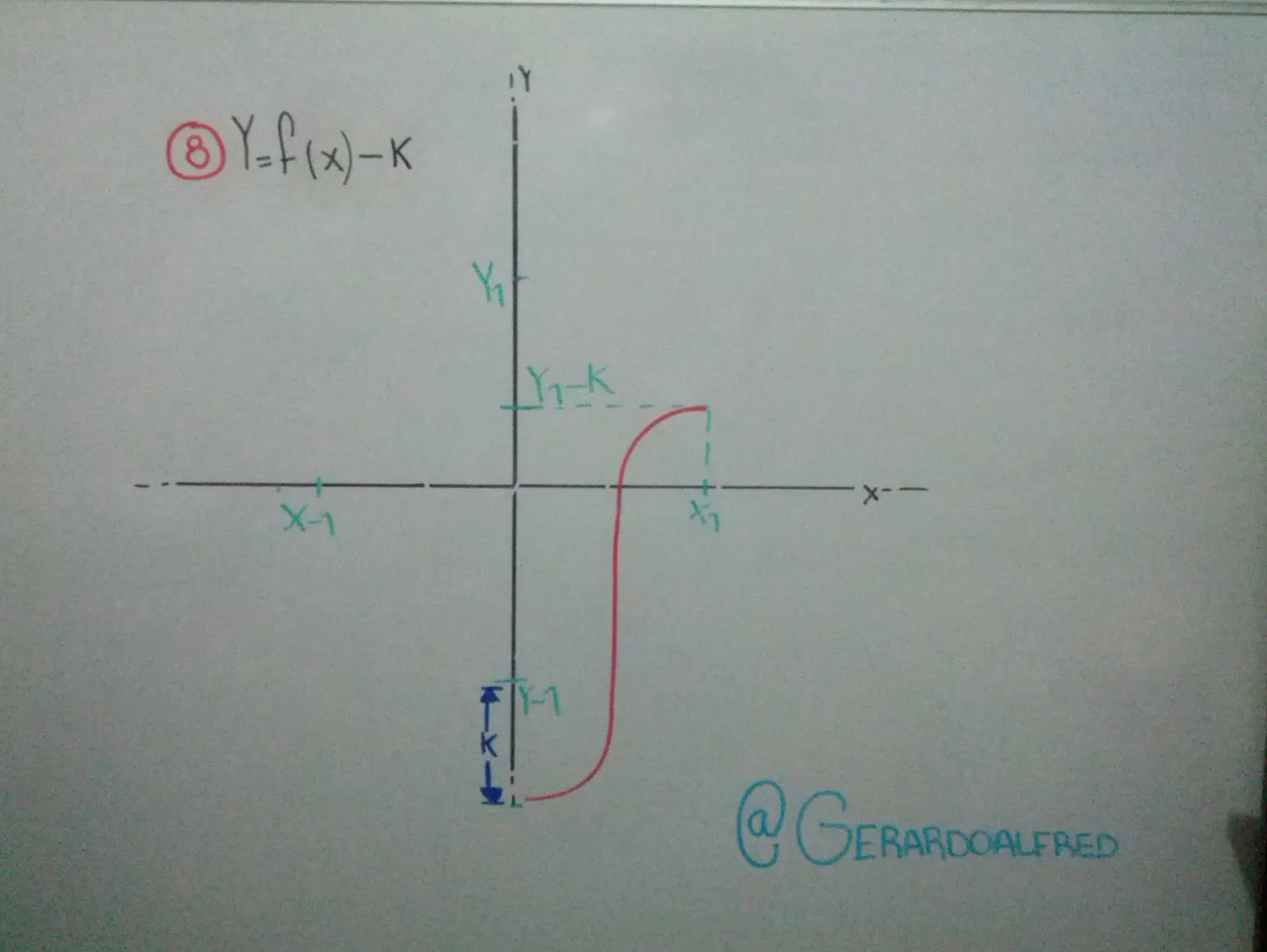
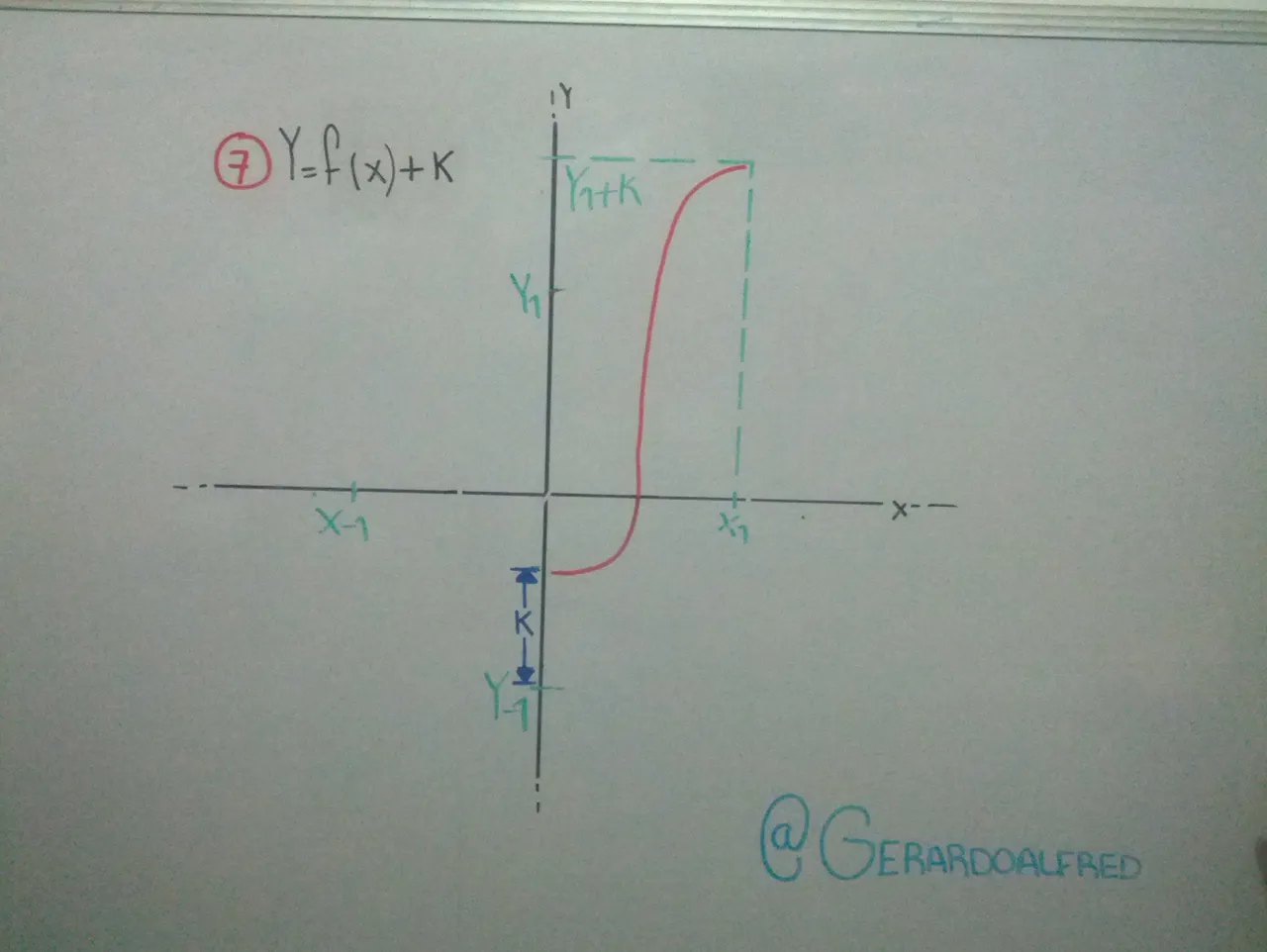
Cuando el valor K esta afuera del argumento F(x) ± K , esto quiere decir que se traslado sobre el eje "Y" (haciendo referencia en las imágenes 7 y 8).
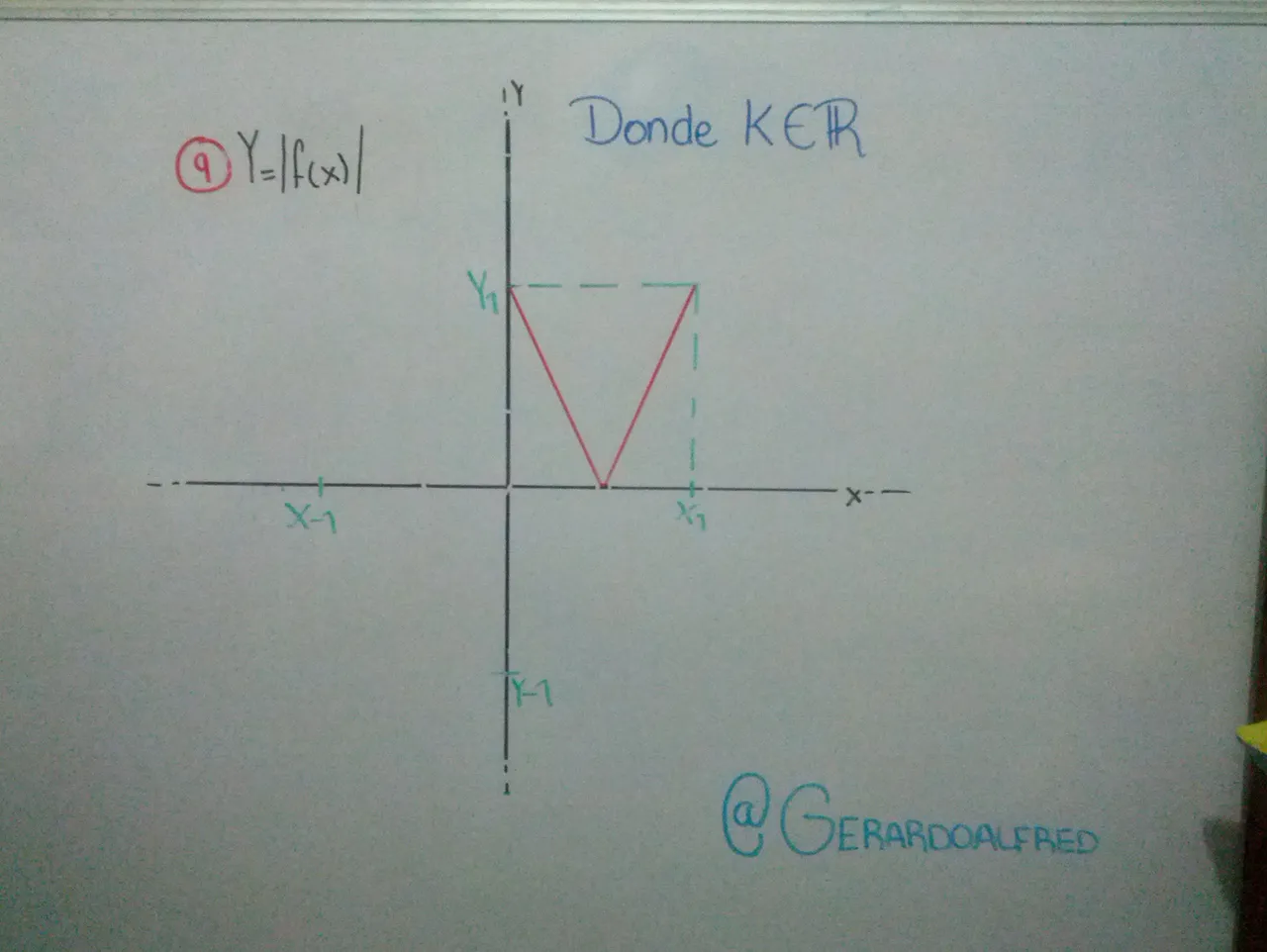
Cuando el valor absoluto abarca toda la función IF(x)I, esto quiere decir todo trazo de curva que este por debajo del eje y se reflejara sobre el mismo (haciendo referencia a la imagen 9).
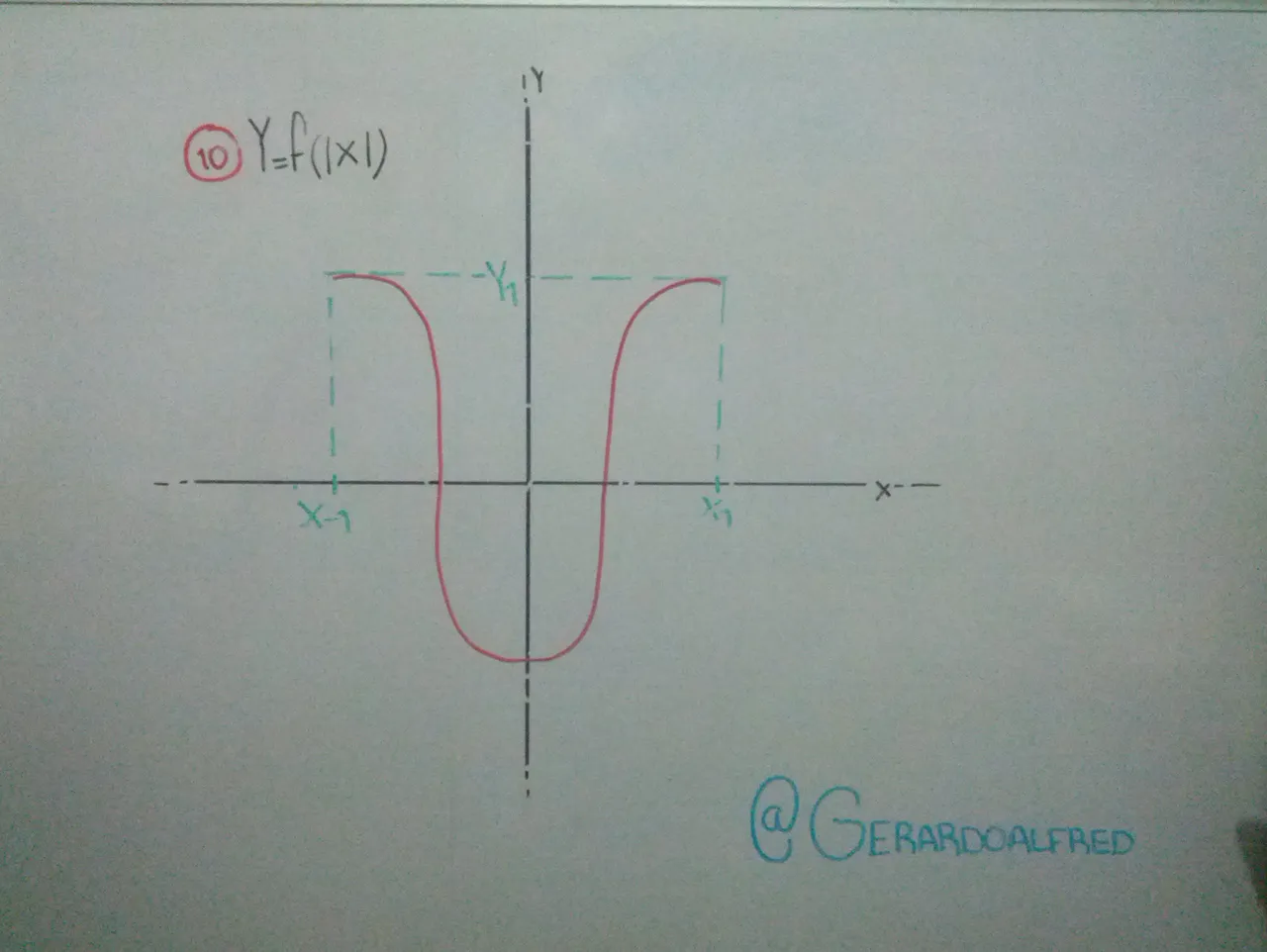
Cuando el valor absoluto solo en el argumento F(IxI), esto quiere decir que la función es simétrica sobre el eje "Y" ( haciendo referencia a la imagen 10 ).
Referencias Bibliográficas
1.-James Stewart (2001). Cálculo de una variable: trascendentes tempranas. 6ta Edición. Editorial Learning cengage
2.-Leithold Louis (200). Cálculo. 7ta Edición . Editorial universidad Iberoamericana.

