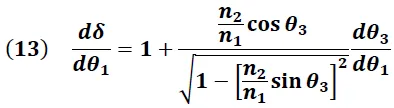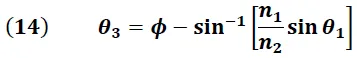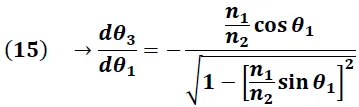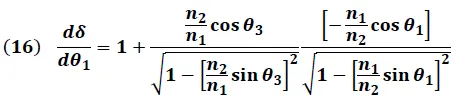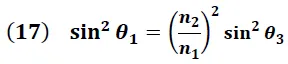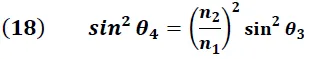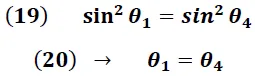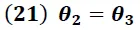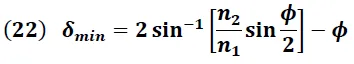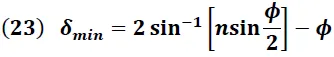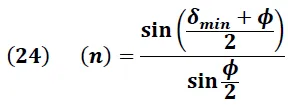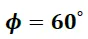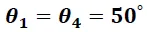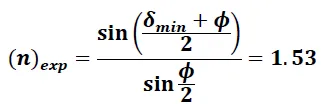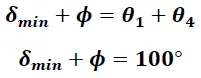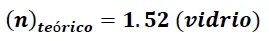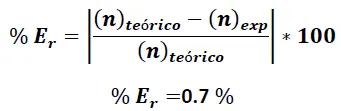¡Hola amigos de Steemit!
Reciban un cordial saludo.
La caracterización de materiales es uno de los objetivos principales hacia donde apuntan una gran variedad de análisis físicos y químicos, apoyados en técnicas que cuentan con equipos de alta tecnología, los cuales facilitan el alcance de dichos objetivos.
El índice de refracción es uno de los parámetros de interés en el análisis y caracterización de un material, debido a su relación con sus propiedades ópticas y estructura electrónica.
La correcta medición de este parámetro es esencial en la industria de los hidrocarburos, plásticos y fabricas de lentes, entre otras, y constituye uno de los elementos primordiales que caracterizan el funcionamiento de una fibra óptica.
Dada su importancia, en esta publicación determinaremos experimentalmente con instrumentos básicos el índice de refracción de un material, con el objeto de afianzar y fortalecer nuestros conocimientos de un parámetro de vital interés en la caracterización de un material.
En nuestro desarrollo experimental, mediremos el índice de refracción de un prisma triangular a partir del ángulo de desviación mínima que experimenta un rayo de luz cuando este atraviesa dicho prisma. Si bien nuestro modelo está limitado a la obtención del índice de refracción de un prisma de vidrio, este modelo puede ser utilizado para la obtención del índice de refracción de distintos materiales.
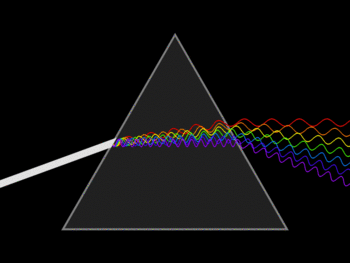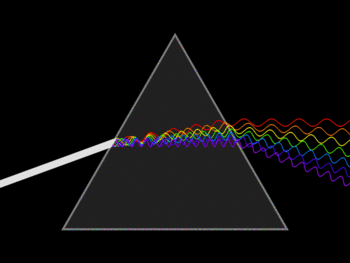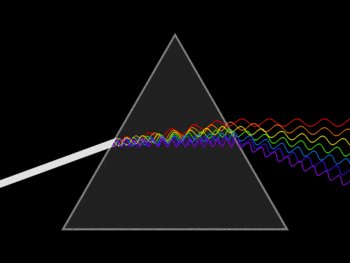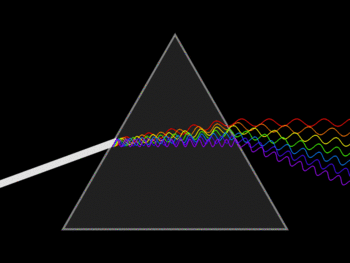 Figura 1 – Desviación de un rayo de luz a través de un prisma de índice de Refracción “n”
Figura 1 – Desviación de un rayo de luz a través de un prisma de índice de Refracción “n”
Wikimedia Commons - Domino Público
Fundamentos teóricos
El cambio en dirección y magnitud que experimenta la velocidad de un rayo de luz o cualquier onda electromagnética cuando incide con un determinado ángulo sobre la interfaz o frontera que separa dos medios con densidades distintas es conocido como refracción.
Este fenómeno de refracción es cuantificado a partir del índice de refracción definido por la expresión:
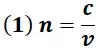
Donde:
c → velocidad de la onda en el vacío = 3.10 8 m/s
v → velocidad de la onda en el medio
La trayectoria y la relación entre las velocidades de los medios constituyentes, está gobernado por la ley de Snell de la refracción, dada por la siguiente expresión:
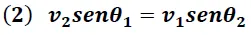
v1 → velocidad de la onda en el medio 1
v2 → velocidad de la onda en el medio 2
θ1 → ángulo de incidencia
θ2 → ángulo de refracción
La ley de Snell expresada en función de los índices de refracción toma la siguiente forma:
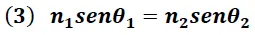
n1 → índice de refracción del medio 1
n2 → índice de refracción del medio 2
La trayectoria del rayo refractado, según lo expresa la ley de Snell, depende de los cambios en los índices de refracción de los medios en los que la onda se propaga.
En la figura 2 se observa el caso de una onda que penetra en un medio con un índice de refracción mayor (n2 > n1). Bajo esta condición, la tendencia del rayo refractado será de acercamiento a la normal del plano (frontera) que limita ambos medios. En caso contrario (n2 < n1), el rayo refractado experimenta una desviación cuya tendencia será de alejamiento a la normal.
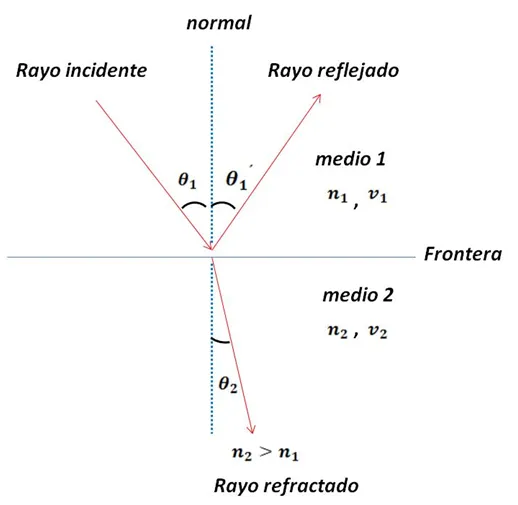 Figura 2 – Diagrama esquemático de la reflexión y refracción de un rayo de luz
Figura 2 – Diagrama esquemático de la reflexión y refracción de un rayo de luz
(Elaborado por @lorenzor en PowerPoint)
Ángulo de desviación mínima "δmin"
En la siguiente imagen se muestra la desviación de un rayo de luz cuando este atraviesa un prisma de vidrio con un ángulo de vértice "ϕ".
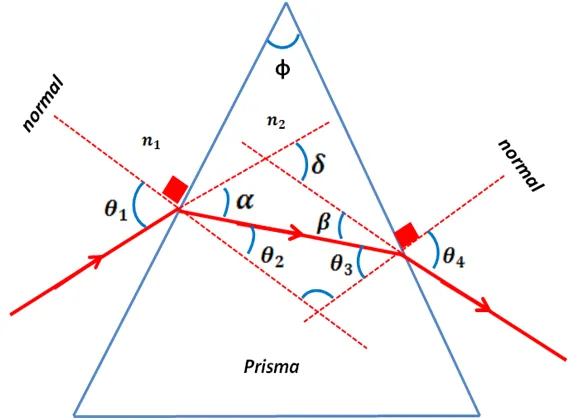 Figura 3 – Diagrama esquemático de la trayectoria de un rayo de luz en un prisma
Figura 3 – Diagrama esquemático de la trayectoria de un rayo de luz en un prisma
(Elaborado por @lorenzor en PowerPoint)
En este sistema el rayo es refractado en la entrada y salida del prisma, tal y como lo establece la ley del Snell de la refracción.
Según la ley de Snell y un análisis geométrico del sistema, se obtiene las siguientes ecuaciones:
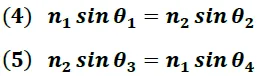
θ3 → ángulo de incidencia en el interior del prisma
θ4 → ángulo de refracción en la salida del prisma
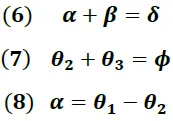
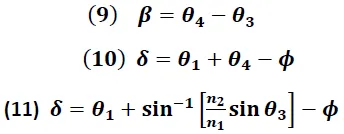
Para una desviación mínima del rayo incidente se debe cumplir que:
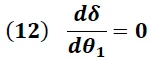
Derivando la ecuación (11) respecto al ángulo de incidencia 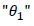 se obtiene:
se obtiene:
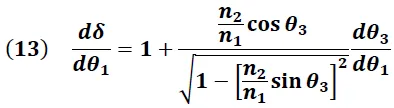
Combinando (7) y (4) se tiene:
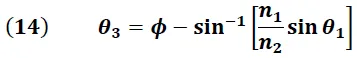
Derivando la expresión (14) respecto a "θ1" obtenemos:
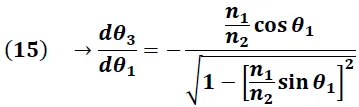
Sustituyendo (15) en (13) se obtiene:
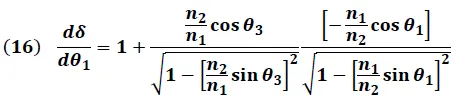
Igualando a cero la expresión (16) y simplificando obtenemos:
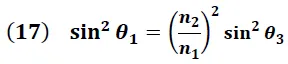
Según la ecuación (5) se tiene que:
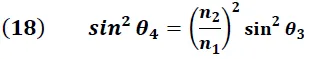
Igualando (17) y (18) se obtiene:
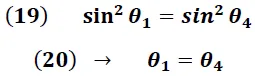
El resultado mostrado en la expresión (20) nos indica que el rayo incidente sufre una desviación mínima cuando los ángulos de entrada y salida del rayo de luz, medidos respecto a sus normales, son iguales.
Este resultado conduce además, según lo expresado por las ecuaciones (4) y (5), a que:
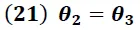
Se puede concluir de nuestro análisis teórico que el camino seguido por el rayo dentro del prisma, bajo la condición de desviación mínima, debe ser estrictamente horizontal, tal y como se muestra en la siguiente imagen.
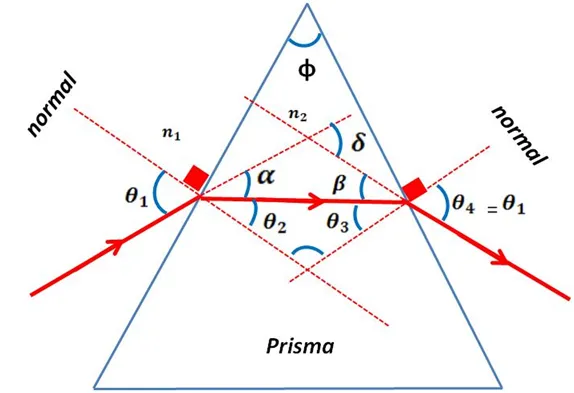 Figura 4 – Trayectoria del rayo de luz bajo la condición de ángulo de desviación mínima
Figura 4 – Trayectoria del rayo de luz bajo la condición de ángulo de desviación mínima
(Elaborado por @lorenzor en PowerPoint)
De los resultados obtenidos en las expresiones (20) y (21), el ángulo de desviación mínima dado por la ecuación (11) se puede expresar de la forma:
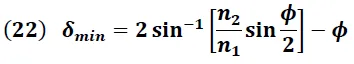
Dado que:
n1 ≈ 1 (Aire)
n2 = n (índice de refracción del prisma)
Podemos expresar la ecuación (22) de la forma:
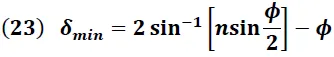
Despejando el índice de refracción "n" se obtiene:
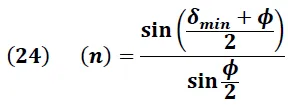
La ecuación (24) permite obtener de manera simple, el índice de refracción del prisma (material) como una función del ángulo de desviación mínima "δmin" y del ángulo de vértice del prisma "ϕ".
Parte experimental
Materiales y equipos utilizados
 Figura 5 – Materiales utilizados
Figura 5 – Materiales utilizados
(Fotografía tomada por @lorenzor en el laboratorio)
Metodología
En nuestro desarrollo experimental seleccionamos un prisma de vidrio a través del cual se hace incidir un rayo de luz (laser) en una de las caras.
Para satisfacer la condición de ángulo de desviación mínima, el ángulo de incidencia del rayo de luz es orientado hasta conseguir que el rayo en el interior del prisma sea horizontal, tal como se muestra en la siguiente imagen.
 Figura 6 – Visualización de la trayectoria del rayo de luz (laser) a través del prisma
Figura 6 – Visualización de la trayectoria del rayo de luz (laser) a través del prisma
(Fotografía tomada por @lorenzor en el laboratorio)
Para una mayor visualización de la trayectoria del rayo a través del prisma, en la siguiente imagen se muestra dicha trayectoria en ausencia de luz.
 Figura 7 – Visualización de la trayectoria del rayo de luz (laser) a través del prisma en ausencia de luz
Figura 7 – Visualización de la trayectoria del rayo de luz (laser) a través del prisma en ausencia de luz
(Fotografía tomada por @lorenzor en el laboratorio)
En el siguiente video se observa en detalle la trayectoria seguida por el rayo de luz.

Video grabado por @lorenzor en el laboratorio
Datos y resultados experimentales
Ángulo vértice del prisma
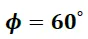
Ángulos de entrada y salida del rayo
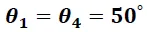
 Figura 8 – Visualización de las medidas experimentales del ángulo de entrada y de salida del rayo de luz
Figura 8 – Visualización de las medidas experimentales del ángulo de entrada y de salida del rayo de luz
(Fotografía tomada por @lorenzor en el laboratorio y editada en PowerPoint)
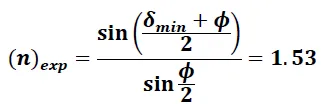
Donde:
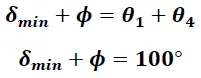
Error porcentual
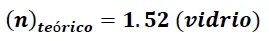
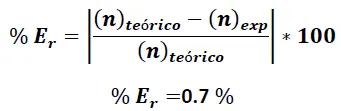
De esta forma podemos apreciar que los resultados obtenidos validan la metodología y los principios físicos utilizados en la determinación del índice de refracción de un material.
Si bien en la actualidad existen técnicas y refractómetros modernos que permiten la obtención del índice de refracción con una alta precisión, estos están soportados bajo los principios físicos aquí expuestos.
Gracias por leer mi publicación. Si tienen alguna pregunta, duda o sugerencia, dejen sus comentarios y con mucho gusto les responderé.
Referencias
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo II. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 2. Addison Wesley Longman.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.
- Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
- Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.

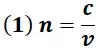
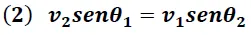
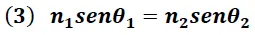


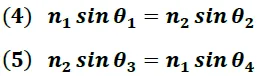
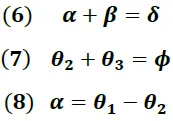
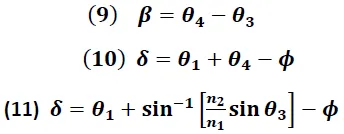
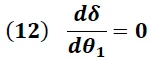
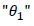 se obtiene:
se obtiene: