En el post anterior les hablé sobre la cicloide, la curva generada por la trayectoria de un punto sobre una circunferencia que rueda sin deslizar sobre una recta y les mostré dos interesantes propiedades de esta, ahora les traigo a la epicicloide; esta se genera igualmente por la trayectoria de un punto sobre una circunferencia, la diferencia radica en que la circunferencia ya no rueda sobre una recta sino en la parte exterior de otra circunferencia, de aca su nombre ( -epi- significa "sobre" y -ciclos- "circulo").
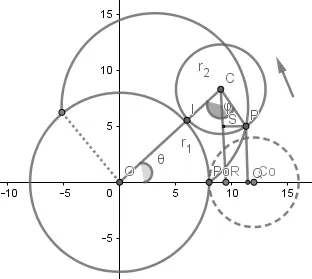
Considerando como origen del sistema de referencia el punto O y como semieje positivo x el que pasa por el punto Po. Siendo Po la posición inicial del punto que describe la curva y Co la posición inicial del centro de la ruleta. El ángulo θ es el que forma la recta de los centros con el semieje positivo x.
Sabemos:
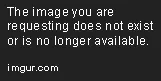
Llamando ϕ al angulo que se forma en PCO, se tiene que:
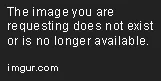
Al despejar phi:
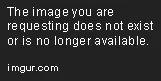
Tambien:
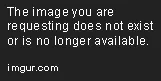
Entonces:
Poniendo que: OC = r1 + r2 ; CP = r2 y ϕ = r1/r2 . θ
obtenemos:
Procediendo de igual forma para "y" :
Poniendo que: OC = r1 + r2 ; CP = r2 y ϕ = r1/r2 . θ
obtenemos:
Resultando ser (1) y (2) las ecuaciones parametricas de la epicicloide.

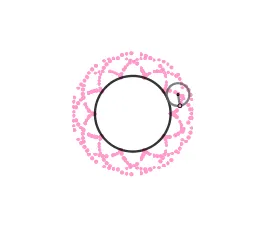
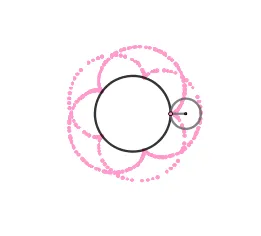
Lo atractivo de la epicicloide son las figuras que se pueden obtener al variar el radio ya sea de la circunferencia directriz o la generatriz, se originan formas como el cardioide, la nefroide y hasta parecidas a una flor. Estás formas vienen dadas por el cociente "k" entre el radio de la circunferencia directriz (la circunferencia por la cual se desliza la circunferencia superior) y la generatriz, cuando el resultado es un número entero obtenemos igual número de cuspides que nuestro cociente, siendo el caso más sencillo cuando k = 1 generando el cardioide, ocurriendo cuando el radio de nuestra circunferencia generatriz es igual al de la circunferencia directriz, en el caso de k = 2 obtenemos la nefroide.
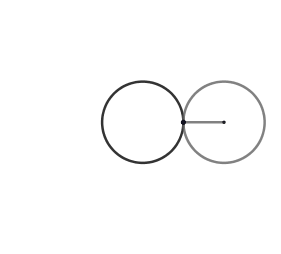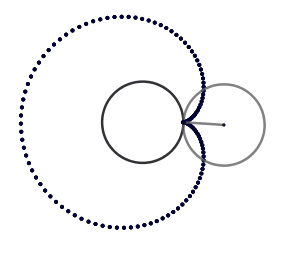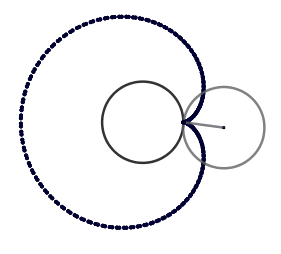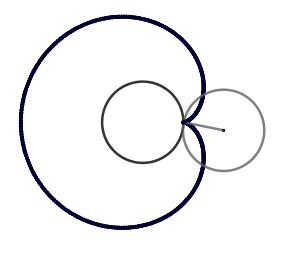
El cardioide debe su nombre a la similitud con un corazón y es también conocido como el corazón matemático. El cardioide además aparece como la envolvente de los rayos de luz reflejados por una superficie circular cuando el foco se encuentra en el borde de esta, esto se conoce como - cáustica - y son zonas donde los rayos de luz se concentran, un ejemplo común es cuando tenemos un vaso con agua que está siendo iluminado y este proyecta sobre la mesa su sombra; en esta hay zonas con curvas brillantes estás curvas son las cáusticas .
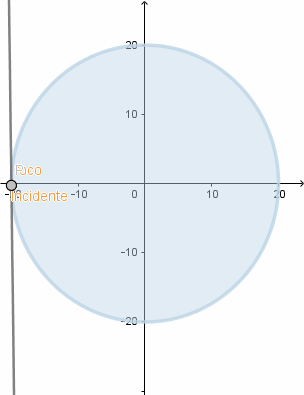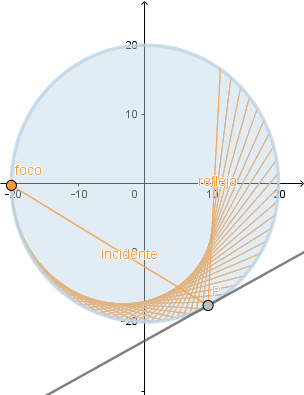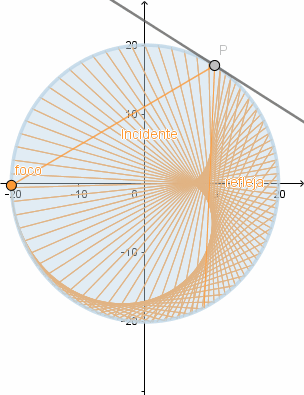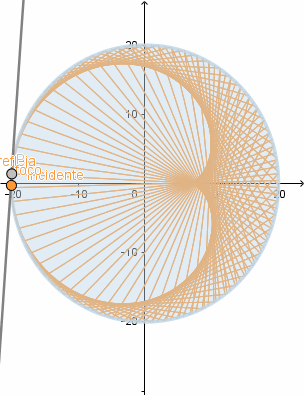

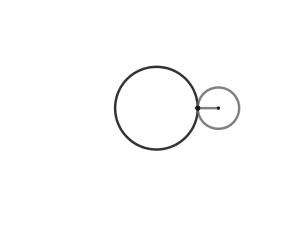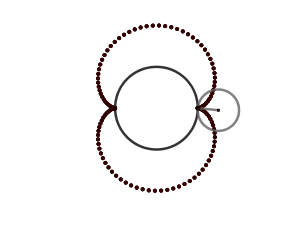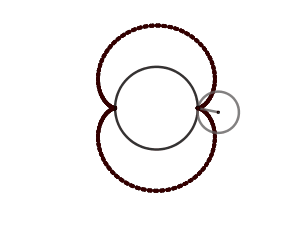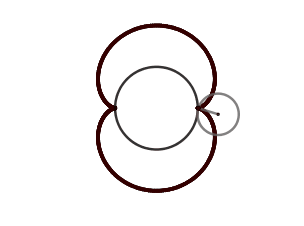
En el caso en el que los rayos sean proyectados por un foco exterior a la circunferencia se crea una cáustica en forma de nefroide.


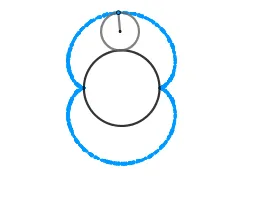
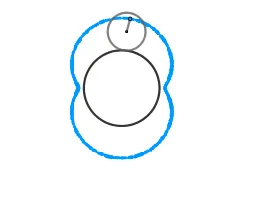
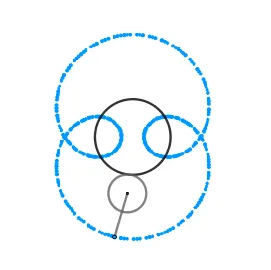
En las imagenes de arriba podemos ver tres nefroides una normal, una acortada y una alargada respectivamente.
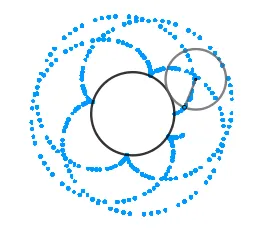
Algunas figuras interesantes que se forman al variar los radios de las circunferencias: