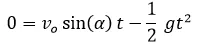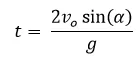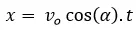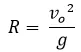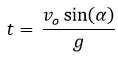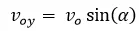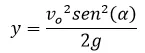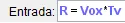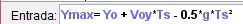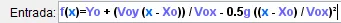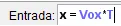(Todas las imágenes y animaciones han sido hechas por mi usando el software matemático GeoGebra Classic 5.)
Saludos queridos lectores, hoy les traigo un tipo de movimiento que está presente en diferentes fenómenos y con el cual hemos tenido contacto a lo largo de nuestra vida; al patear un balón, al batear o lanzar una pelota, todos estos ejemplos tiene algo en común y es que al ser lanzados con cierto ángulo respecto al eje horizontal sus trayectorias terminan describiendo una parábola y por eso se le conoce como movimiento parabólico.
A continuación haremos un estudio de este movimiento enfocado en el lanzamiento de proyectiles logrando una deducción de las ecuaciones que lo rigen y para continuar con el aprendizaje del software GeoGebra integraré en este mismo artículo lo que he venido haciendo por separado, mostrar cómo realizar la simulación de un fenómeno, en este caso del movimiento parabólico para así ir avanzando en el dominio del software.
Para el estudio de este movimiento haremos uso de un modelo idealizado en el cual se desprecia la fricción debida al aire, la curvatura de la tierra y su rotación; al estar inmerso en un plano de dos dimensiones solo consideraremos la aceleración vertical que este sufre debido a la gravedad la cual será siempre constante en magnitud y dirección, la componente x de la aceleración es cero por lo tanto en el eje x el proyectil describe un movimiento con velocidad constante y en el eje y uno con aceleración constante dado como dije antes por la gravedad, ademas se considera que en t = 0 el proyectil se encuentra en x = 0 e y = 0.
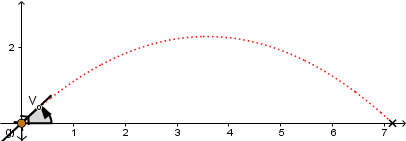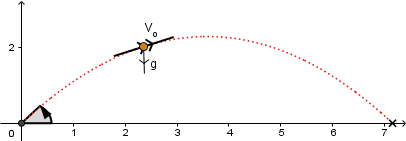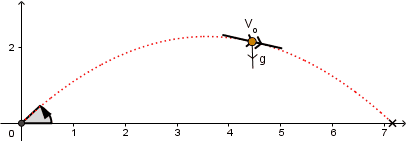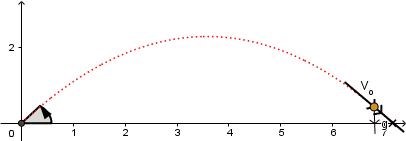
El vector velocidad de la partícula siempre es en todo punto tangencial a la trayectoria.
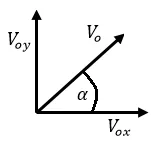
Teniendo en cuenta lo anteriormente dicho podemos descomponer al vector velocidad en sus componentes y tratar el problema por separado aplicando la segunda ley de Newton:
Para el eje x.
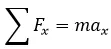
Al tratarse de un movimiento a velocidad constante tenemos:
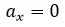
Por lo tanto:
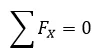
Sabemos que:
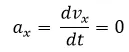
Por lo tanto:
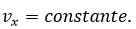
Del triangulo que se forma podemos ver que:
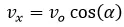
Para el eje y.
Aplicando la segunda ley de Newton:
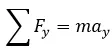
Sabemos que la aceleración es igual a la gravedad, entonces:
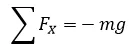
Vemos que:
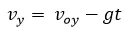
Y sabemos que:
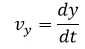
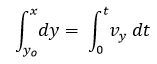
El resultado de lo anterior es:
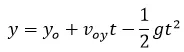
(1)
Alcance del proyectil.
Podemos determinar a que distancia aterrizará el proyectil a partir de las ecuaciones encontradas anteriormente, para esto supondremos que el proyectil aterriza a la misma altura de la cual partió.
Recordemos que:
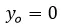
Por lo tanto:
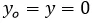
Al sustituir lo anterior en (1) y recordando que 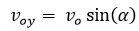 obtenemos:
obtenemos:
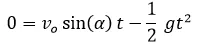
Hecho lo anterior procedemos a despejar "t" lo cual por ser una ecuación de segundo grado tiene dos soluciones, la primera es cero lo cual corresponde cuando el objeto partió de la posición inicial y la segunda es:
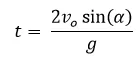
Esta solución corresponde al tiempo que tarda en caer el proyectil y se le conoce como
tiempo de vuelo (tv)
el cual nos permite saber a que distancia caerá el proyectil sustituyendo esa expresión en:
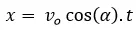
Al sustituir y realizar las operaciones correspondientes obtenemos el alcance del proyectil:
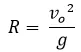
Altura máxima.
Anteriormente encontramos el tiempo que tarda el proyectil en completar su trayectoria (tiempo de vuelo), la altura máxima que alcanza el proyectil se da justo en la mitad de la trayectoria por ende el tiempo que tarda en llegar ahí es la mitad del tiempo de vuelo y se le conoce como
tiempo de subida (ts):
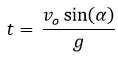
Recordando que la velocidad es 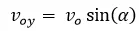
(1)
y realizar las operaciones correspondientes obtenemos la altura máxima que alcanza el proyectil:
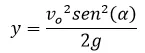

Ejemplos.
¿Qué ocurre si la gravedad es cero?
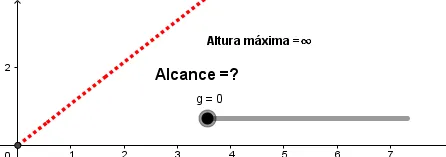
Como podemos ver el proyectil ya no describe una parábola; la trayectoria es una recta ascendente debido a que no hay ninguna fuerza externa que se oponga al movimiento de este.
Aumentando la gravedad.
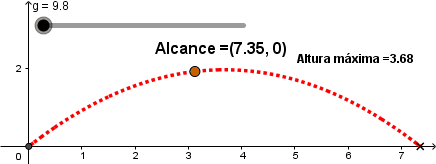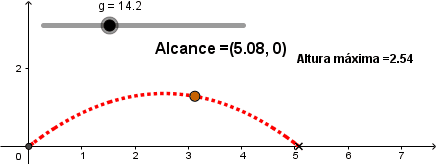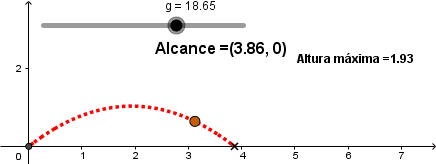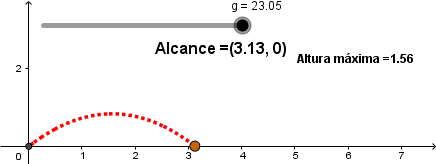
En la animación anterior vemos la variación de la trayectoria a diferentes valores de la gravedad, empezando con la gravedad de la tierra y terminando con una fuerza de gravedad similar a la de Júpiter. Como se observa a una mayor fuerza de atracción gravitacional el alcance del proyectil disminuye, llegando a tierra más rápido.
Disminuyendo la gravedad.
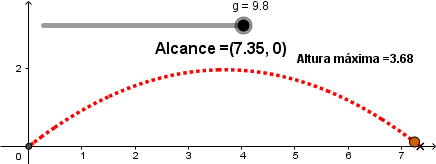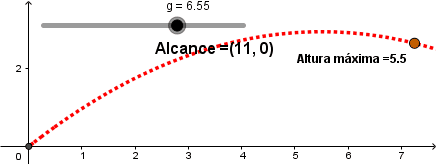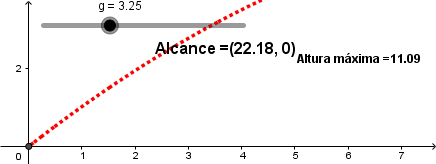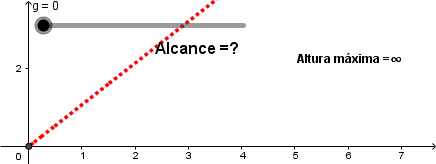
En el caso contrario como es de esperar el alcance aumenta, al disminuir la gravedad el proyectil en su trayectoria describe parábolas más amplias.
Aumentando la velocidad inicial.
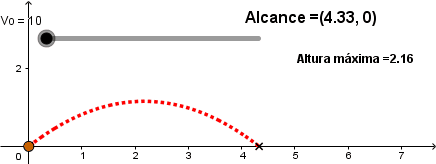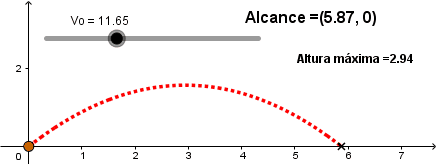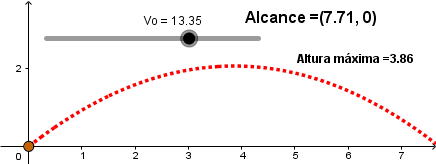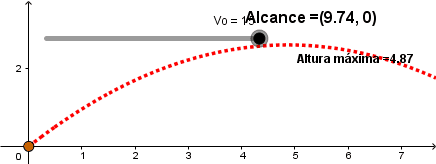
Como podemos ver a mayor velocidad inicial el proyectil alcanza una mayor distancia lo cual concuerda con nuestra experiencia diaria al lanzar una pelota.
Variando el ángulo de lanzamiento.
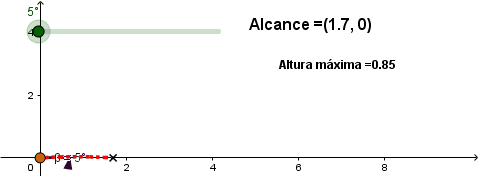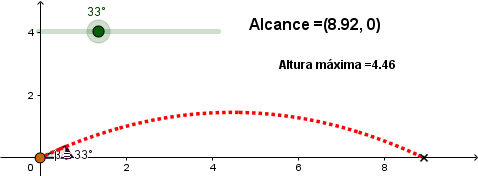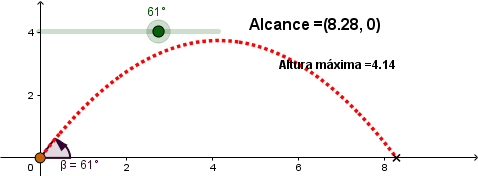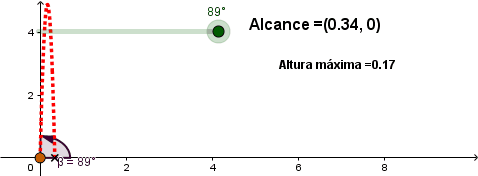
Al aumentar el ángulo de lanzamiento de 0 a 45° el alcance aumenta y en el intervalo de 46° a 90° empieza a disminuir, se observa que el máximo alcance se logra con un ángulo de lanzamiento de 45°.

Pasos para crear la simulación con GeoGebra Classic 5.
Empezaremos creando deslizadores para el tiempo, la gravedad, la velocidad inicial y el ángulo de lanzamiento:
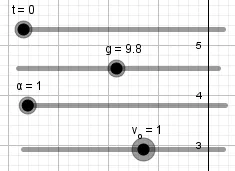
Para el tiempo el intervalo del deslizador será de 0 a tv
y para el ángulo de 0 a 90.
Luego de esto escribiremos en la barra de entrada cada ecuación que rige el movimiento parabólico.
Empezamos con la velocidad.
Para el eje x:

Para el eje y:

tiempo de vuelo:

Tiempo en llegar al punto más alto:
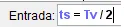
Alcance:
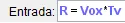
Altura máxima:
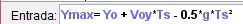
Luego de esto escribimos la función que rige el movimiento parabólico (nuestra parábola).
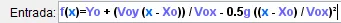
El resultado es el siguiente:
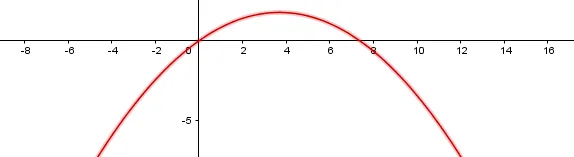
Como vemos nuestra parábola es muy grande así que debemos delimitar el área de interés, para esto usaremos el comando "función" con las siguientes características:

En
expresión colocaremos
f
en
valor inicial 0
y en
valor final R
obteniendo como resultado la siguiente curva:
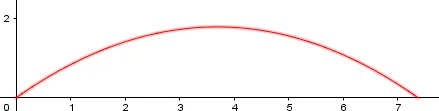
Hecho lo anterior procederemos a crear un punto que intercepte a esta curva y el eje y para esto vamos a la segunda ventana de la barra de herramientas y seleccionamos la opción intersección. Luego de seleccionada hacemos click sobre la curva y después sobre el eje y, hacemos lo mismo para el eje x y obtenemos lo siguiente:
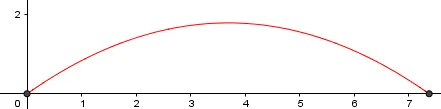
Estos puntos representan el punto de salida y el punto de llegada. Ahora para crear nuestro proyectil crearemos una recta con definición 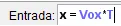
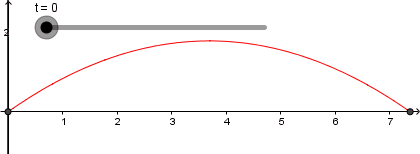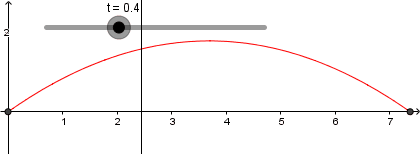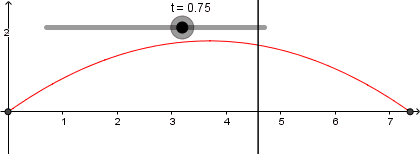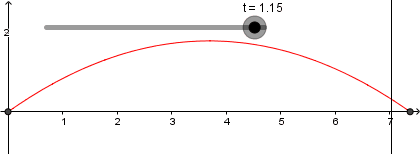
En los puntos donde esta recta y nuestra parábola se interceptan es la trayectoria que seguiría nuestro proyectil, así que usaremos de nuevo la herramienta de intercepción sobre la recta y la parábola para crear este punto:
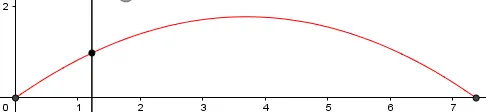
El resultado de todo lo que hemos hecho hasta ahora es lo siguiente:
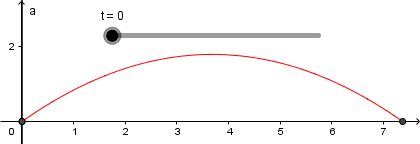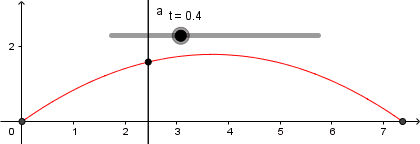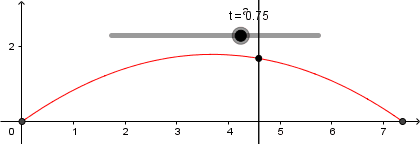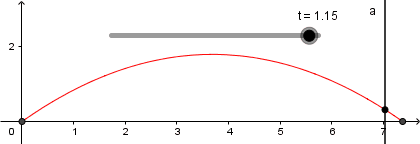
Llegado a este punto ya tenemos nuestra simulación lista, solo debemos ocultar los objetos no deseados, agregar colores, estilo de líneas entre otros:

Terminada nuestra simulación podemos empezar a interactuar con ella variando la velocidad, el ángulo de lanzamiento, la altura, la gravedad y responder todas nuestras incógnitas sobre cómo varía la trayectoria del objeto al cambiar estas variables.
Conclusiones generales:
En el movimiento parabólico en el eje x el proyectil describe un movimiento a velocidad constante.
En el movimiento parabólico el proyectil describe un movimiento con aceleración constante en el eje y debido a la gravedad.
El vector velocidad es tangencial a la trayectoria.
El tiempo de vuelo es el tiempo que tarda el proyectil en completar su trayectoria.
El tiempo que tarda el proyectil en llegar al punto más alto es igual a la mitad del tiempo de vuelo.
En el punto más alto de la trayectoria la velocidad vertical es cero.
El mayor alcance del proyectil se logra al lanzarlo con un ángulo de 45° respecto a la horizontal.
A menor gravedad el alcance del proyectil aumenta y si la gravedad aumenta el alcance disminuye.
Mientras mayor sea la velocidad inicial del proyectil el alcance será mayor.
Material consultado:
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Young, H. D, & Freedman, R. A. FISICA UNIVERSITARIA, volume 1. Pearson Educación de México, S.A. de C.V., 2009.
(Todas las imágenes y animaciones han sido hechas por mi usando el software matemático GeoGebra Classic 5.)

Espero hayan disfrutado de este post y la aplicación de este maravilloso software.
Para leer contenido de calidad sobre ciencia los invito a visitar la etiqueta #stem-espanol.

Imagen creada por @djredimi2



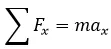
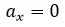
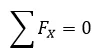
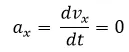
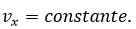
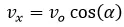
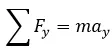
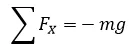
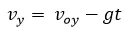
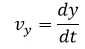
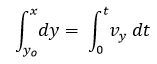
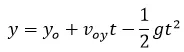
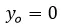
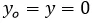
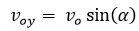 obtenemos:
obtenemos: