Saludos cordiales, amigos de Steemit.
Siguiendo con la serie de presentaciones relacionadas con el álgebra vectorial a continuación presento mi tercer artículo, éste corresponde a la segunda parte del uso de recursos didácticos; en ésta oportunidad expondré un método para explicar el traslado de un vector en el espacio al origen del sistema de coordenadas cartesianas. Para realizar la experiencia es necesario tener conocimiento de los dos artículos anteriores los cuales pueden acceder en los siguientes links: Artículo 1 y Artículo 2.
Traslado de un vector en el espacio al origen de un sistema de coordenadas cartesianas.
Comenzaremos representando un vector en el espacio colocando en cualquier lugar del mesón de laboratoro un soporte universal y sujetamos a éste una flecha de acero (vector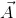 
) (Ver figura 1a), luego colocamos en una esquina nuestro sistema de referencia cartesiano representado por los tres ejes coordenados 
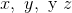(Ver figura 1b).
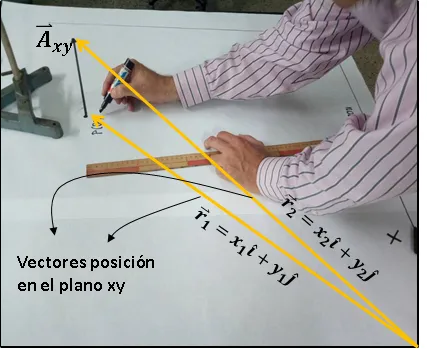
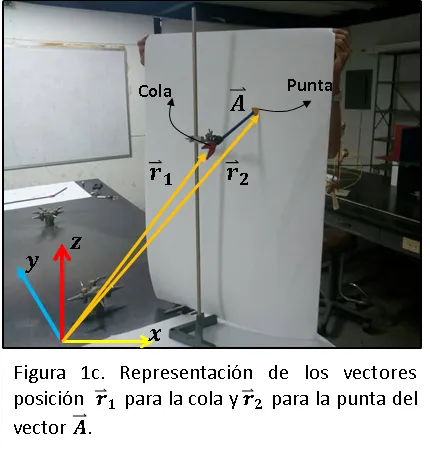
Luego explicamos a los estudiantes la importancia del vector posición, resaltando que este es un vector que siempre sale del origen del sistema de coordenadas y su punta se posiciona en un punto determinado. En este caso los vectores posición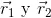 
posicionan la cola y la punta del vector 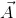respectivamente (Ver figura 1c) y vienen representados por las siguientes ecuaciones:
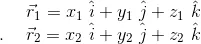
A continuación procedemos a hallar el vector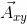 
que no es más que la proyección del vector 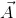sobre el plano 
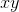. Para hacer esto procedemos tal y como se explicó en el Artículo 2 (Ver vector proyección en el Artículo 2), y dibujamos los puntos correspondientes a su cola y punta. (Ver figuras 2a y 2b).
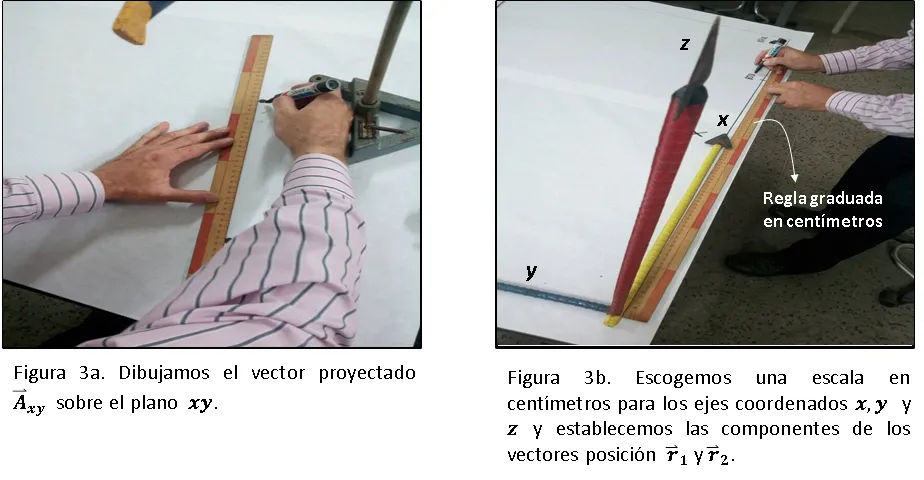
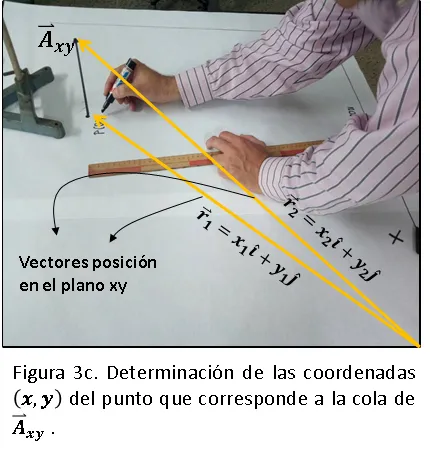
Unimos los dos puntos que corresponden a la cola y la punta del vector proyectado y de esa manera dibujamos el vector 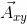, luego escogemos una escala, en este caso en centímetros, de los ejes coordenados de nuestro sistema de referencia y de esa manera ubicamos las coordenadas de la cola y la punta del vector 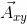, estos serán las magnitudes de las componentes de los vectores posición 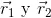, (Ver figuras 3a, 3b y 3c)
Una vez realizado estos procedimientos debemos determinar las alturas o las componentes en el eje 
de la cola y la punta del vector 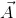en el espacio, después de esto tenemos las tres componentes de los vectores posición en el espacio, para este caso hemos obtenido :
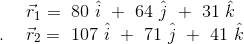
Este paso se debe realizar de tal manera que los estudiantes puedan observar como se hacen las mediciones respectivas de cada coordenada, tomando en cuenta la escala establecida en los ejes coordenados de nuestro sistema de referencia cartesiano. (Ver figuras 4a, 4b y 4c).
Luego hallamos las componentes del vector 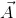, las cuales se calculan de la siguientes manera:
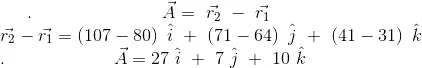
Una vez habiendo calculado las componetes del vector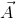 
pasamos al paso final, este consiste en sacar la flecha de los ganchos (que representa el vector 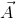en el espacio) y tratando de conservar la misma dirección se traslada al origen del sistema de coordenadas, esto se hace simplemente ubicando el punto calculado 
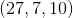que corresponde a la punta del vector 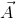. Al colocar el vector en el origen del sistema el estudiante apreciará que el vector no se alteró para nada, ni en dirección, ni en magnitud. (Ver figuras 5a y 5b).
Una vez realizada esta experiencia el estudiante entenderá la importancia de los vectores posición ya que son ellos los que nos permite trasladar un vector en el espacio al origen del sistema de coordenadas, también sabrá que para poder operar con un vector es necesario que se calculen sus componentes en cada uno de los ejes coordenados y para obtener esto debemos trasladarlo al origen del sistema que estemos utilizando.
Otra experiencia interesante es que el estudiante puede comparar lo que ha calculado con un hecho real, y este se manifiesta al ver que sus número coinciden con un resultado vivencial, él puede apreciar que los procedimientos matemáticos se pueden llevar a la realidad física.
Mi experiencia ha demostrado que los estudiantes asimilan mucho mejor los conceptos y las operaciones matemáticas por medio del uso de estos recursos didacticos, el alumno se siente estimulado o motivado al experiementar este tipo de cosas en el laboratorio o en cualquier otro lugar. La participación activa del estudiante es fundamental a la hora de aplicar este tipo de métodos para el aprendizaje del álgebra vectorial.
Hasta la próxima entrega... espero sus valiosos comentarios y sugerencias sobre este método.
Muchísimas gracias.
Referencias.
[1] Feynman R. P., Leighton R., Sand M. Física. Mecánica, radiación y calor, Addison-Wesley Iberoamericana, Wilmington, Delaware, USA, 1987.
[2] VerLee L., Aprender con todo el cerebro, Martínez Roca, Colombia, 1997.
[3] Kittel Ch., Knight W., Ruderman M., Mecánica, Serie Berkeley, Vol. 1, Reverté, Barcelona, 1989.
[4] Young H. Freedman R., Física Universitaria, 12da. ed., Addison-Wesley, México, 2009.