La interpretación analítica que realicé en la publicación anterior daba cuenta del estudio de un cuerpo cilíndrico, donde consideramos al volumen del cilindro como una función que depende del radio y altura de este sólido geométrico. Para hacer más sencilla la explicación, consideré una altura h = 5 cm como una constante y trabajamos con el radio entre 1 y 10 cm para ver la razón de cambio en el volumen a medida que aumentamos esta variable, concluyendo que la derivada de esa función sería una línea tangente o pendiente de la curva V(r, 5).

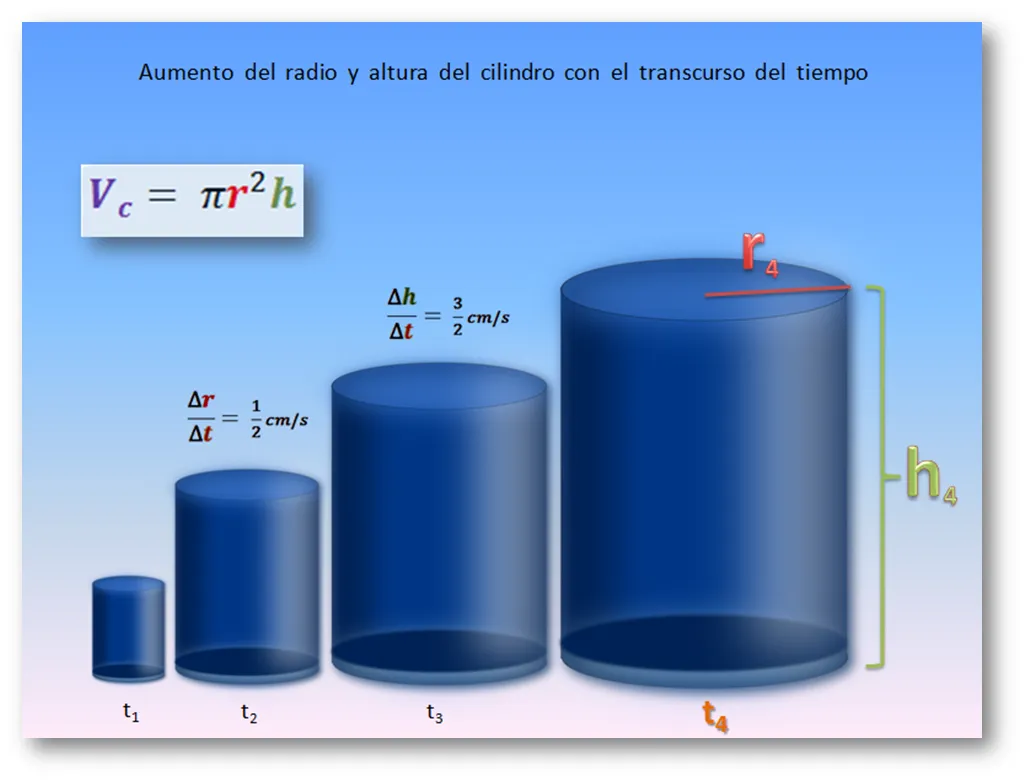
En el caso que este cuerpo geométrico sufra variación del volumen con una tasa de cambio del radio en 0,5 cm/s, mientras que la altura del cilindro varía a razón de 1,5 cm/s, entonces podemos echar mano del cálculo diferencial para determinar la razón de cambio de la función escalar (volumen) con respecto al tiempo, esto es dV_c/dt

Es notorio que el volumen del cilindro, puede ser considerado como una función de 2 variables, V_c(r, h) = πr²h, por lo que se puede aplicar La Regla de la Cadena para estudiar la influencia de pequeños incrementos del tiempo sobre los valores intermedios de las variables "r" y "h", o sobre los valores finales del V_c.

Note que para calcular la tasa de cambio del volumen del cilindro con respecto al tiempo, debemos considerar el par de variables (r, h) con su respectiva rapidez de incremento, 0,5 cm/s en r y 1,5 cm/s en h.

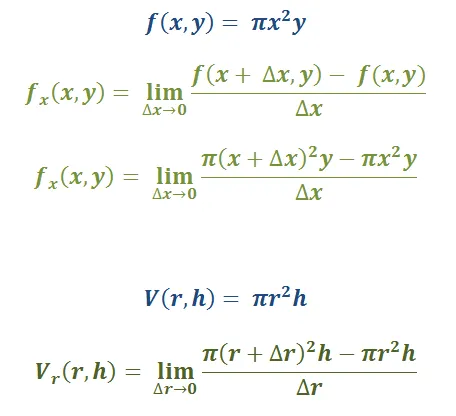
Recordemos que la derivada de una función está relacionada con el estudio de las tendencia de esa función, por lo que podemos analizarla a través de la definición de límite. Esto también aplica para las derivadas parciales!

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de Jills: Portada de mujer y fórmulas matemáticas
• Nota Academia: La regla de la cadena multivariable
• Wikipedia: Derivada parcial

Con los números enteros positivos o los naturales
podemos hacer algunos cálculos básicos
con la derivación e integración entera de funciones escalares