Cuando tenemos sólidos conocimientos de las operaciones matemáticas aplicadas a la potenciación y funciones, entonces estaremos en capacidad de resolver los problemas combinados de estos 2 temas. Las igualdades en Matemática se cumplen sí o sí, por ejemplo: 2 + 2 = 4, además ya están establecidos los procedimientos metodológicos para demostrarlas, existiendo la posibilidad de obtener el mismo resultado (4) a partir de otras operaciones algebraicas y aritméticas sencillas o complejas. En este artículo veremos la manera de combinar las reglas de los exponentes con una ecuación de 2 variables.

En las áreas de Física, Química, Biología e Ingeniería se trabaja frecuentemente con números que se repiten múltiples veces o que son muy grandes sus cantidades, por lo que se recurre a la notación exponencial y normalmente consiste en expresar un número que se multiplica varias veces (n veces) elevado al exponente n, en forma matemática: Xⁿ = X·X·X·X··(n veces)

Regla de la potencia: (X^m)ⁿ = X^m·n

, resulta de colocar la misma base y multiplicar los exponentes.

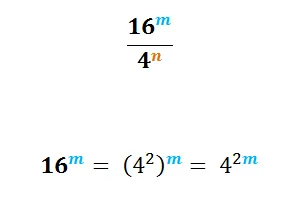
En este paso también aplicamos la definición de la Potenciación: Xⁿ = X·X·X·X··(n veces) = P , que no es más que multiplicar el número base "n" cantidad de veces que lo indica el exponente, en este caso: (4²) = 4·4 = 16

Regla del cociente: X^m/Xⁿ = X^m−n

, resulta de colocar la misma base y restar los exponentes.

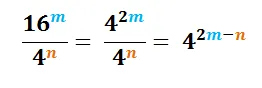
El lenguaje matemático es claro, sencillo y contundente, y vemos que aplicando las reglas de la potenciación podemos escribir el cociente original de otra manera que no sea una división.

Trabajando la ecuación de 2 variables

Estamos en plena libertad de realizar las operaciones matemáticas que se nos ocurran, siempre y cuando respetemos las reglas matemáticas y que no existan restricciones, tanto en la potenciación como en la igualdad de la ecuación planteada. Lo que sí debemos tener claro es que estamos buscando una forma de relacionar ambas expresiones matemáticas para hallar la solución apropiada.

---

Este resultado es agradable a mi vista, porque es la misma expresión que el exponente de 4 en la primera relación, esto es: 4^{2m − n}

---

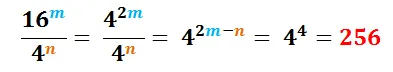
Con agrado y satisfacción puedo exclamar ¡Voilà!

Las multiplicaciones sucesivas de un mismo número pueden expresarse en notación exponencial y las reglas que gobiernan la Potenciación de los números reales pueden aplicarse para resolver cualquier tipo de relación de variables que intervengan en la base o en el exponente de esta notación, como lo hemos visto en el ejemplo que he desarrollado.

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de geralt: Portada con el problema planteado
• Guía de aprendizaje: Reglas de los Exponentes
• Blog: Potenciación y sus propiedades
• Blog: Leyes de los exponentes
• Profesor en línea: Potenciación: Leyes o Reglas de los exponentes

Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad,
así que invariablemente encontraremos alguna solución