StemQ Notice: The following is an answer to this question
General version of the problem
I am going to answer this question in a more general form. Denote by R the radius of the sphere , by c the rate constant of evaporation, and denote by h the height of the water level with respect to the bottom of the semi-spherical cup. So R,c will be constants but h will be a variable, more specifically, a dependent variable and the independent variable is of course time which I will denote by t. Then, the aim is to find a formula for h(t).
Overview
Here is an image of the whole setup:
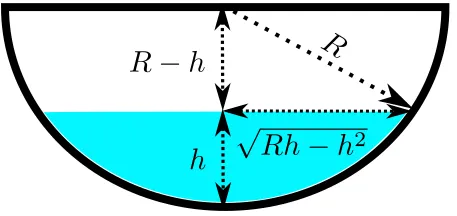
I did a bit of geometry in the image. This might help readers which want to write out all the details of the equations that will follow.
Equations
The surface area of the water at water level h is a function of h so let's denote the area by A(h). The water-volume at water level h can also be written as a function h so denote the volume by V(h). With some basic (and tedious) calculus we can write formulas for both:

Then the equation which relates the volume to the area is given by:
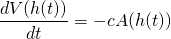
This is a first order differential equation. Straightforward computation using pretty basic calculus yields the solution h(t) = h(0) - ct (where h(0) is the water level at t=0). Observe that the equation is elegant in the sense that it is very simple. This is pretty cool.
Note that the equation only makes sense for h(t) greater or equal to zero. More specifically, when h(t)=0 all the water has evaporated.
Intuition
Intuitively, the solution formula h(t) = h(0) - ct makes sense since even without doing any calculus we expect that V(h) ~ c_1 h^3 and A(h) ~ c_2 h^2. So then according to the differential equation h(t) ~ c_3 t.
The result without equations
Stripping the math from this blog post our final results tells us that the water level goes down at a constant speed. :o)
StemQ Notice: This post was originally submitted on StemQ.io, a Q&A application for STEM subjects powered by the Steem blockchain.