As additional support for my previous post on functors, I want to throw in this less technical example.
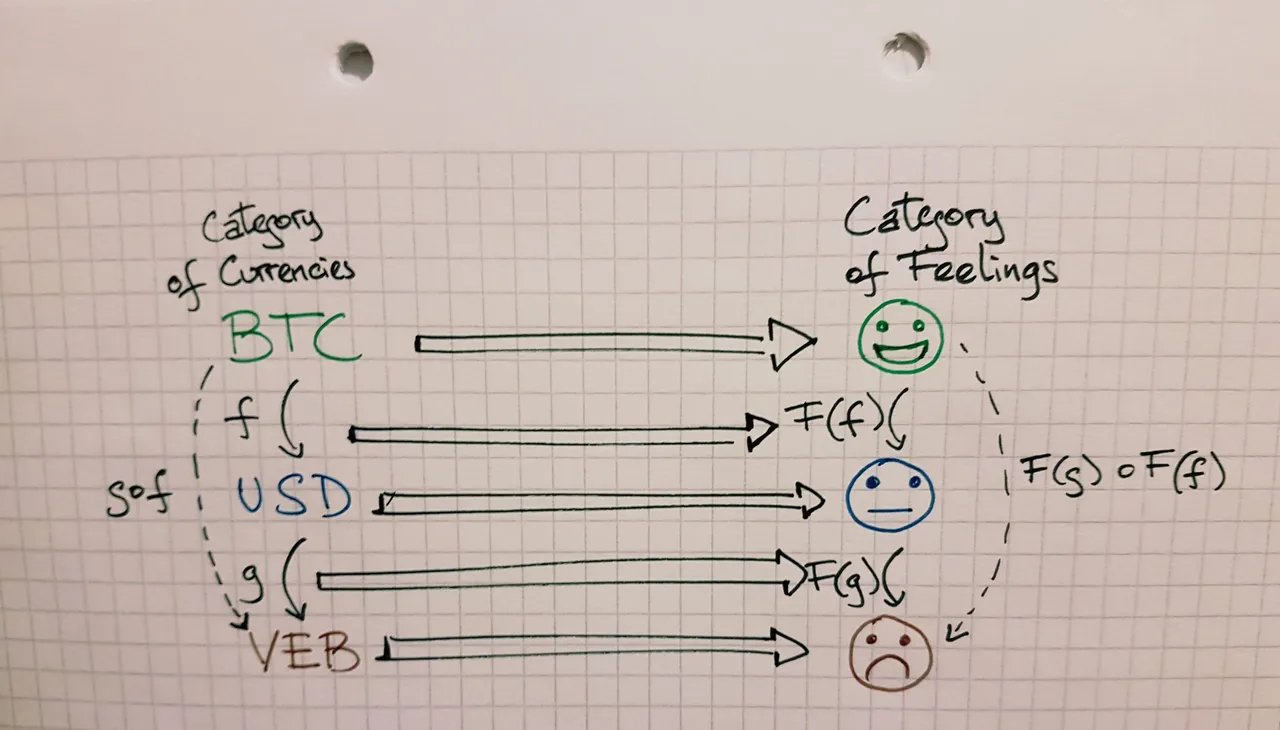
As you can see in the drawing, we have the following:
- A little world of transformations between things (currencies), called "Category of currencies"
- Another little world of transformations between things (feelings), called "Category of feelings"
- "f" and "g" are just generic names for transformations (give them any meaning you want.)
The point is that a functor is a sort of "meta" transformation.
It transforms a category into another category, i.e. a world of transformations into another world of transformations, in a way that makes sense.
What do I mean by "in a way that makes sense"?
In the drawing, all those fat horizontal arrows in the middle are doing the meta transformation. I.e. they're putting each object and transformation in the right place.
For example, we see that:
- BTC gets mapped to happy feeling.
- USD gets mapped to neutral/meh feeling.
In light of that, it makes sense that "f" (which goes from BTC to USD), gets transformed into a function from happy feeling to neutral/meh feeling.
Of course, saying "it makes sense" is a hand-wavy thing. The mathematical definition of functor is actually precise. But I'm just giving you some more intuition. I hope it helps!