
This is a Turkish Python tutorial about numerical methods. I will write about how can we use python programming language for our math problems especially numerical methods.
Euler Teoremi Nedir?
Eğer çok yüzlünün herhangi iki noktasını birleştiren doğru parçası yine bu yüzlünün içinde kalıyorsa, bu çok yüzlüye konveks (dışbükey) çok yüzlü denir. Konveks çok yüzlülerin yüz, ayrıt ve köşe sayıları arasında Euler Teoremi olarak bilinen bir bağıntı vardır. [Wiki]
e^iπ + 1 = 0 denklemine Euler denklemi denilir. e, i ve π birbirinden farklı değerlere ve kullanım alanlarına sahipken Euler denkleminin sonunda hepsi ortak bir tam sayıya indirgenip eşitlenmiş oluyor. Matematiğin bazı insanlara güzel gelen o harmonisi bu sanırım.
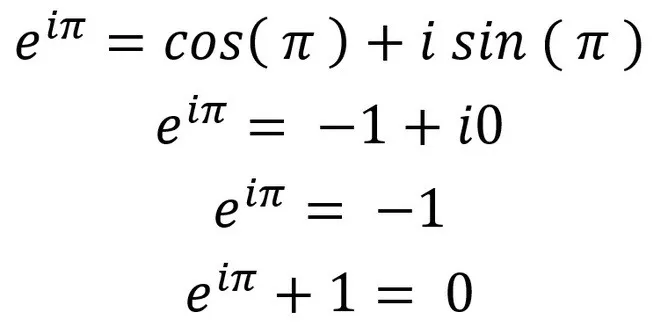
source | Euler Denklemi

source | Tylor Açılımı
Fakat bu yazıda Euler'ın güzelliğine veya matematiksel çözüm-ispatına değinmek yerine bunu Python ile nasıl birleştiririz, Python ile bir Euler denklemini nasıl çözeriz ona değineceğiz.
Python ile Euler Çözümü
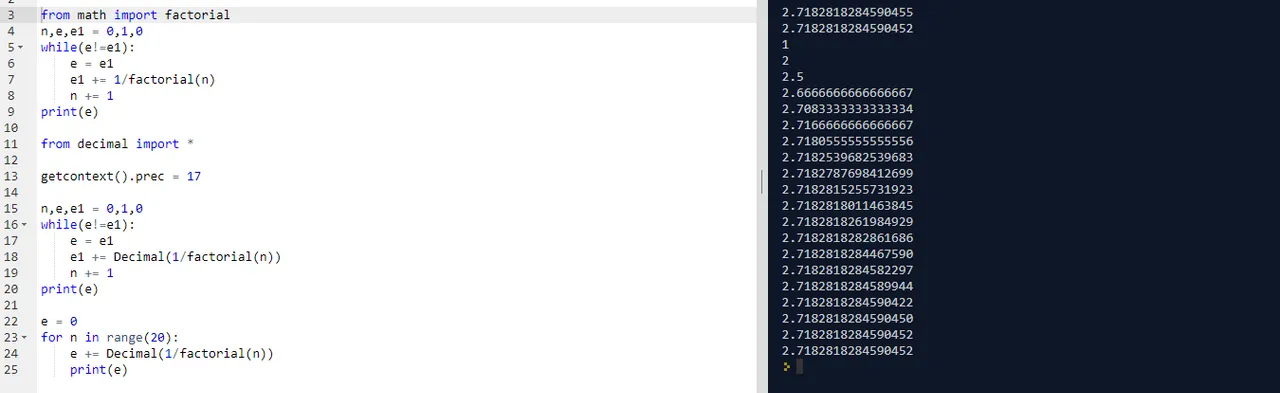
Kod örneğimizde de gördüğünüz gibi e sayısını hesaplarken ilk hesaplamada standart python kitaplığı kullanılırken ikinci hesaplamada decimal modülü kullandık. Tüm bu işlem sonucunda iki farklı çıktı aldık ve bunlar sırasıyla
2.7182818284590455
2.7182818284590452
oldular. Peki bu çıktılara nasıl ulaştık? Yazdığımız kod tam olarak ne yaptı adım adım inceleyelim bunu.
Öncelikle math kütüphanesinden factorial metodunu import ederek başladık yazdığımız koda. Ardından n,e,e1 adlı değişkenlerimizi oluşturup bunların başlangıç değerlerini atadık. Bu değerler elbette rastgele değiller, yapacağımız işlemlere yönelik sabit ilk adım değerleri bunlar. Ardından 1 iterasyonda elde edilecek çıktıyı bulabilmek için Euler formülüne uygun bir şekilde matematiksel işlemleri koda döküyoruz.
from math import factorial
n,e,e1 = 0,1,0
Her defasında n'i 1 arttırarak onun 1/factorial 'ini alıyoruz. Bu işlem e ve e1 birbirine eşit olana kadar devam ediyor. Eşitlik sağlandığında ise while döngüsünden çıkıyoruz. Arından decimal kütüphanesini de import edip aynı işlemi tekrar ediyoruz. Tek fark bu defa e1 += 1/factorial(n) yerine e1 += Decimal(1/factorial(n)) yapıyor oluşumuz.
İkinci while döngüsünden de çıktığımızda artık her bir iterasyonda elde edilen çıktıları göstermemiz kalıyor geriye. Bunu da basit bir for döngüsü ile hallediyoruz.
e = 0
for n in range(20):
e += Decimal(1/factorial(n))
print(e)
Yani yazdığımız kodun çalışma şekli genel olarak bu şekilde. Her bir iterasyonu tek tek bulup ardından onları ekrana yazdırıyoruz.
Posted on Utopian.io - Rewarding Open Source Contributors