Repository
https://github.com/jankulik/AI-Flappy-Bird
What Will I Learn?
- You will learn the basics of neural networks
- You will learn what are the components of perceptron
- You will learn what is the decision-making process of perceptron
- You will learn how perceptron can learn itself
Difficulty
- Basic

Source
Overview
In one of my recent articles I presented a simple AI model that learns itself to play Flappy Bird. Today, I would like to take a closer look on how this model works from the technical side and learn the basics of neural networks. In the first episode of this tutorial I will discuss the general concept of perceptron, its core components and the learning algorithm. In the second episode I will show how to implement those concepts into Java code and build a fully fledged neural network.
Here is a video showing the learning process of this AI:

Perceptron - the simplest neural network
Human brain can be defined as an incredibly sophisticated network containing 86 billion neurons communicating with each other using electrical signals. Brain as a whole is still an elaborate and complex mistery, but structure of a single neuron is already quite exhaustively researched. Simplistically, dendrites receive input signals and, accordingly to those inputs, fire an output signals through synapses.

Source
My Flappy Bird AI model is based on the simplest possible neural network - perceptron. In other words, a computational representation of a single neuron. Similarly to the real one, it receives input signals and contains a processing unit, which provides output accordingly.
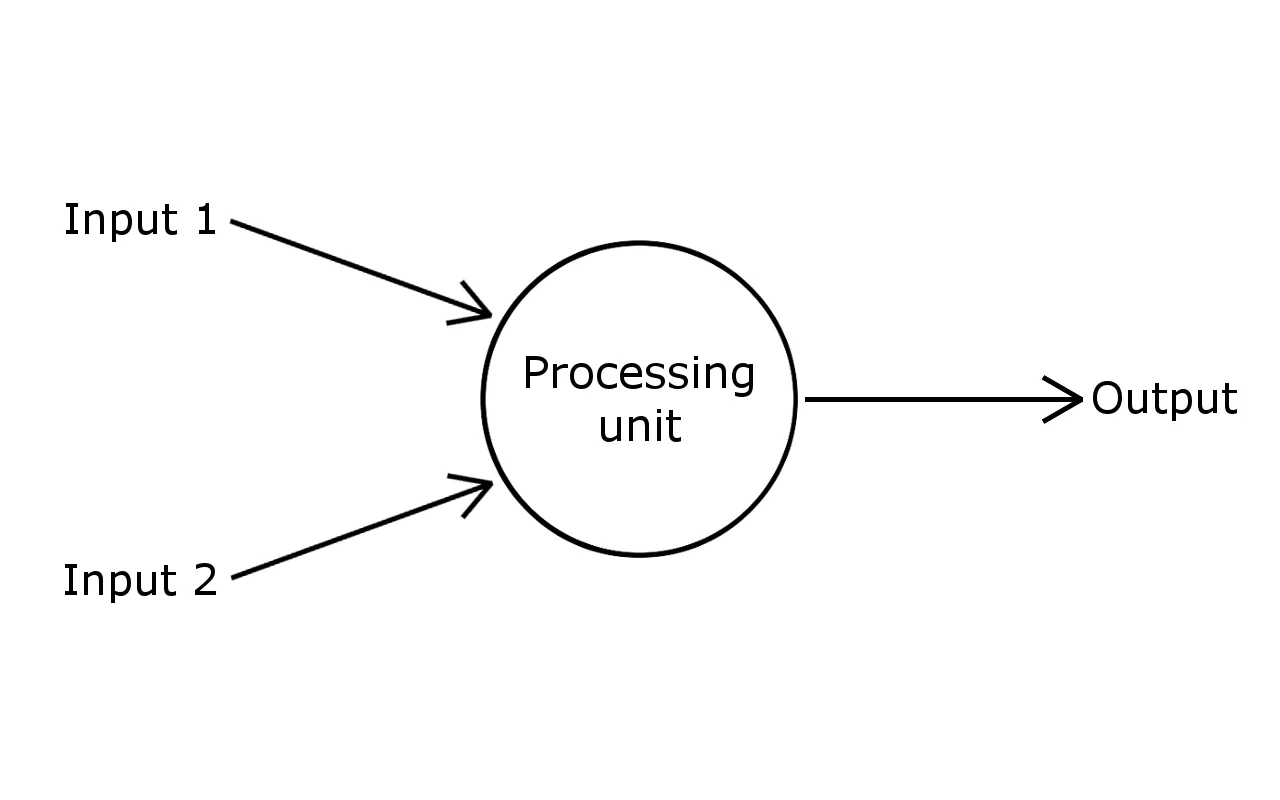
Components of perceptron
Inputs
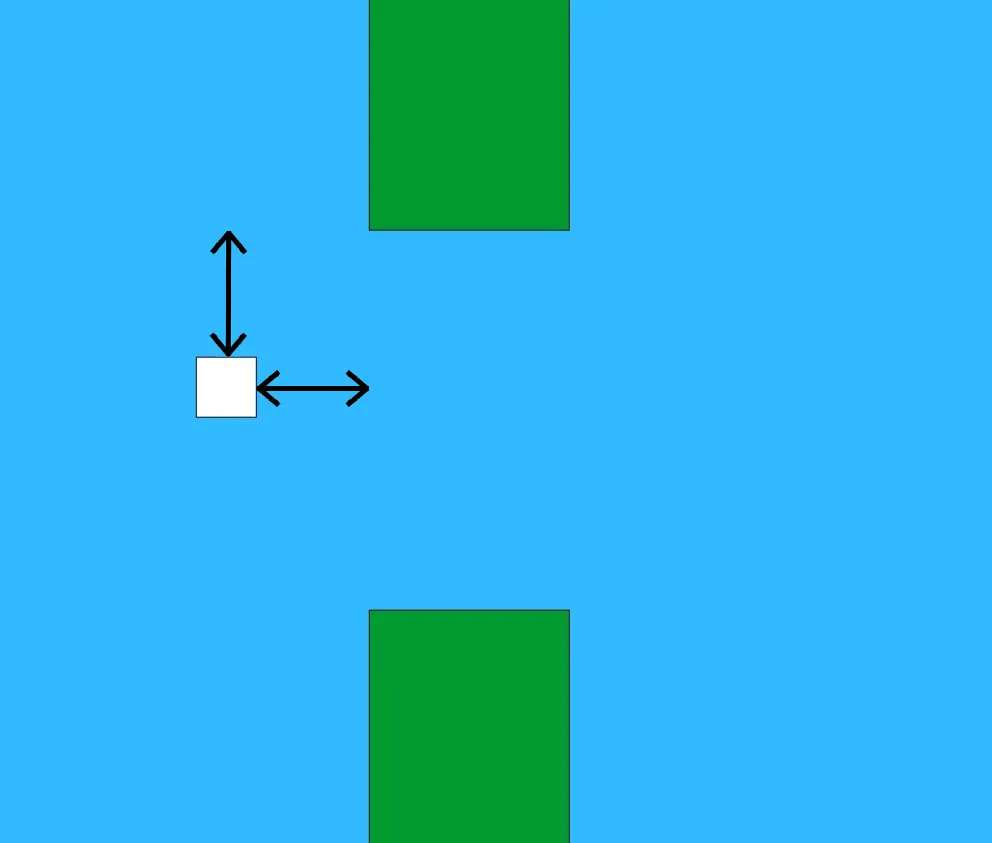
Inputs are numbers that allow perceptron to perceive the reality. In case of my model there are only 2 inputs:
horizontal distance between bird and the pipe
vertical distance between bird and the upper part of the pipe
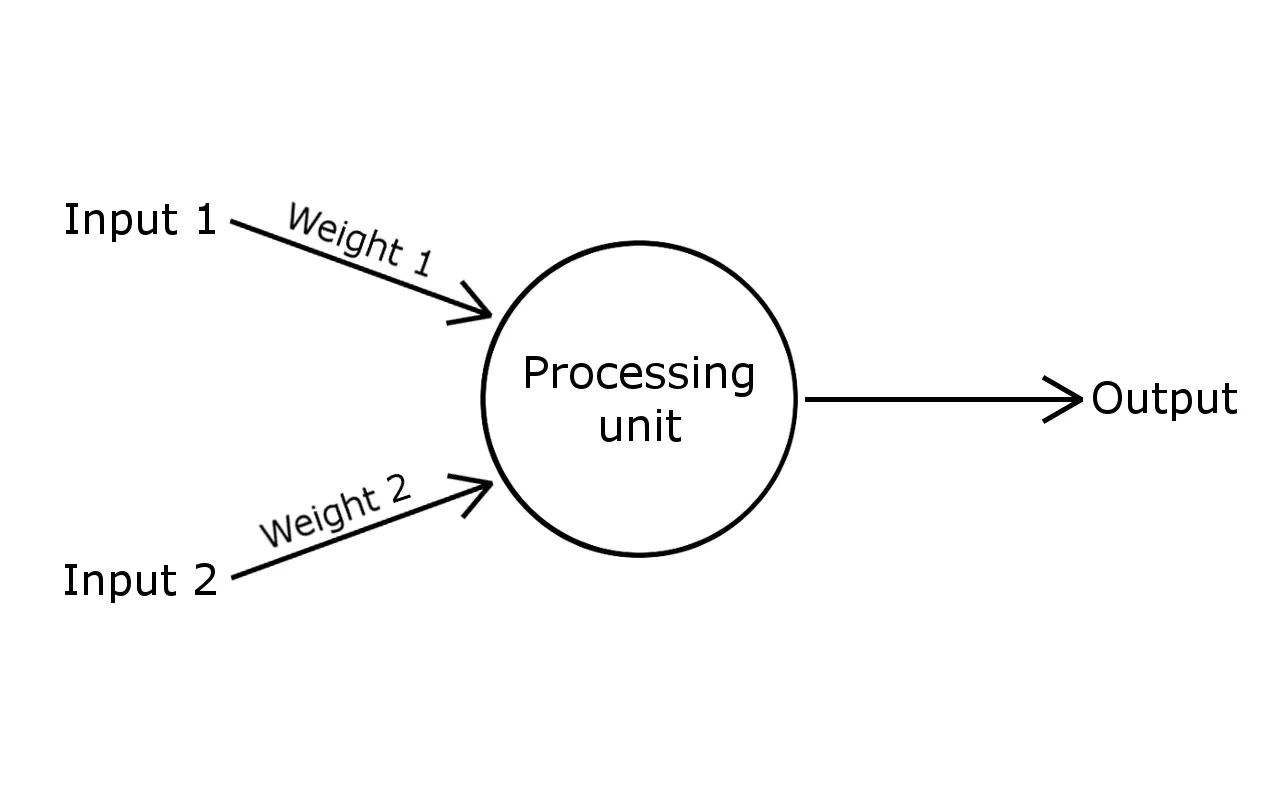
In order to create an adaptive and self-learning model, each input needs to be weighted. Weight is a number (usually between -1 and 1) that defines how the processing unit interprets particular input. When perceptron is created, weights are assigned to each input randomly, then they are modified during a learning process in order to achieve the best performance.
Processing unit
Processing unit interprets inputs according to their weights. Firstly, it multiplies every input by its weight, then it sums the results. Let's assume we have such inputs and randomly generated weights:
Input 1: 27
Input 2: 15
Weight 1: -0.5
Weight 2: 0.75
Input 1 * Weight 1 ⇒ 27 * -0.5 = -13.5
Input 2 * Weight 2 ⇒ 15 * 0.75 = 11.25
Sum = -13.5 + 11.25 = -2.25
For such inputs and weights our processing unit will return the value of -2.25.
Output
The final output of the perceptron in our case should be binary (true or false), as it needs to decide whether to make the bird jump or not. In order to convert our sum (in our example -2.25) into such output, we need to pass it through activation function. In this case it may be really simple: if sum is positive it returns true, if sum is negative it returns false.
Sum = -2.25
Sum < 0 ⇒ Output = false
Under such circumstances our bird would not perform a jump.
Bias
Situation becomes more complicated when the value of both inputs is equal to 0:
Input 1: 0
Input 2: 0
Weight 1: -0.5
Weight 2: 0.75
Input 1 * Weight 1 ⇒ 0 * -0.5 = 0
Input 2 * Weight 2 ⇒ 0 * 0.75 = 0
Sum = 0 + 0 = 0
In that case, regardless of the value of weights, the processing unit will always return a sum equal to 0. Due to that, activation function will not be able to properly decide whether to perform a jump or not. A solution to this problem is bias, which is an additional input with a fixed value of 1 and its own weight.
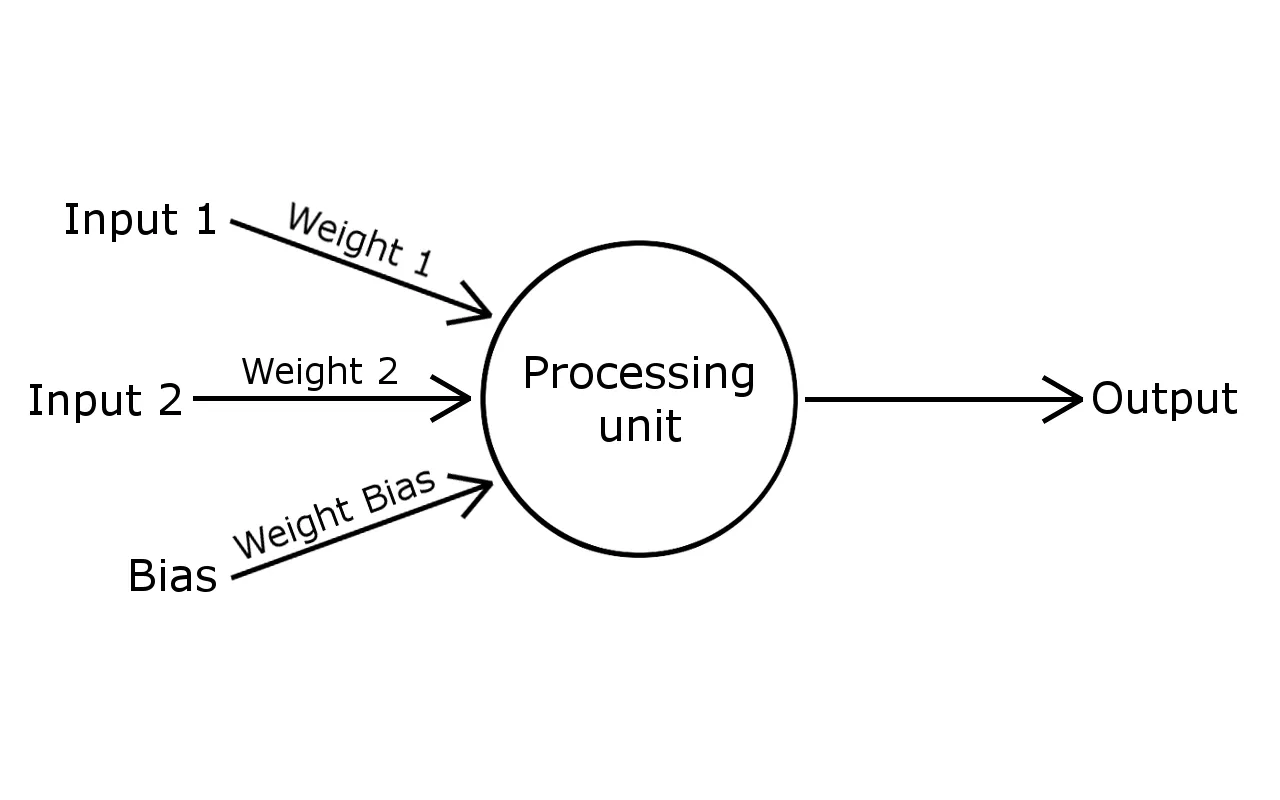
Here are the results of sum with bias (remember that bias is always equal to 1, but its weight may be any number):
Input 1 * Weight 1 = 0
Input 2 * Weight 2 = 0
Bias * Bias Weight ⇒ 1 * Bias Weight = Bias Weight
Sum = 0 + 0 + Bias Weight = Bias Weight
In that case, bias's weight is the only factor having impact on the final output of the perceptron. If it is a positive number bird will perform a jump, otherwise it will continue falling. Bias defines the behavior and perceptron's understanding of reality for inputs equal to 0.
Learning process
If bird had collision with the pipe, it implies that its perceptron made some wrong decision. In order to avoid such situation in the future we need to adapt the perceptron by adjusting its weights. The output of our perceptron is binary, so there are only 2 possibilities:
bird collided with the upper pipe - it probably jumps too often; output is too often true - weights need to be decreased.
bird collided with the lower pipe - it probably jumps too seldom; output is too often false - weights need to be increased.
Weights can be easily adjusted using the following equation:
New Weight = Current Weight + Error * Input * Learning Constant
Error can be described as a difference between expected and actual behavior. In our case error will equal to
1or-1, thus defining if weights will be increased or decreased. If we need to increase weights (bird jumps too seldom) error will be equal to1, if we want to decrease weights (bird jumps too often) error will be equal to-1.Input assigned to weight that we are modifying. We need to consider input in the moment of bird collision.
Learning Constant is a variable that defines how rapid will be the change in the value of weights, thus controlling the pace of learning. The bigger learning constant is, the faster Perceptron learns, but with the smaller precision. In the Flappy Bird model I have used
0.001as a learning constant.