오랜만에 수학, 상수와 관련된 책을 읽었다. 페르르 베크만의 파이의 역사란 책인데, 상당히 오래된 책이다.

이 책은 고대 시대부터 현대에 이르기까지 사람들이 어떻게 Pi를 계산했는가에 대해 다루고 있다.
수학에는 여러가지 유명한 상수들이 있다. 아마 그 중에 가장 대중들에게 유명한 상수는 pi 가 아닌가 싶다. 3.14159265359 ..... 이 끝도 없이 계속되는 무한 소수는 인류의 문명과도 함께할 정도로 우리에게 매우 친숙한 숫자이다.
지난번에 여러 수학 기호들에 대한 연도 조사를 했었는데, 알고보니까 Pi의 기호가 생각보다 오래되지 않았다. 관련글-[자료 모음] 기호의 역사
기호는 1706년에 정해졌다고 하지만, 실상 이 Pi 의 계산은 메소포타미아에서부터 시작된다. 농업혁명 이후, 영토를 제대로 나누기 위해서 이런 Pi 값을 구했다고 한다.
이집트 사람들은 메소포타미아 사람들보다는 덜 정확하지만 간단한 방식으로 Pi 값을 구했는데 이는 정사각형을 가지고 계산한 것으로 후에 아르키메데스는 정96각형을 가지고 더 정확한 Pi 값을 계산했다. [책의 중반부에 유도과정이 등장한다.] 관련 포스팅 -[수학] pi 데이
대략 그림을 그려 본다면
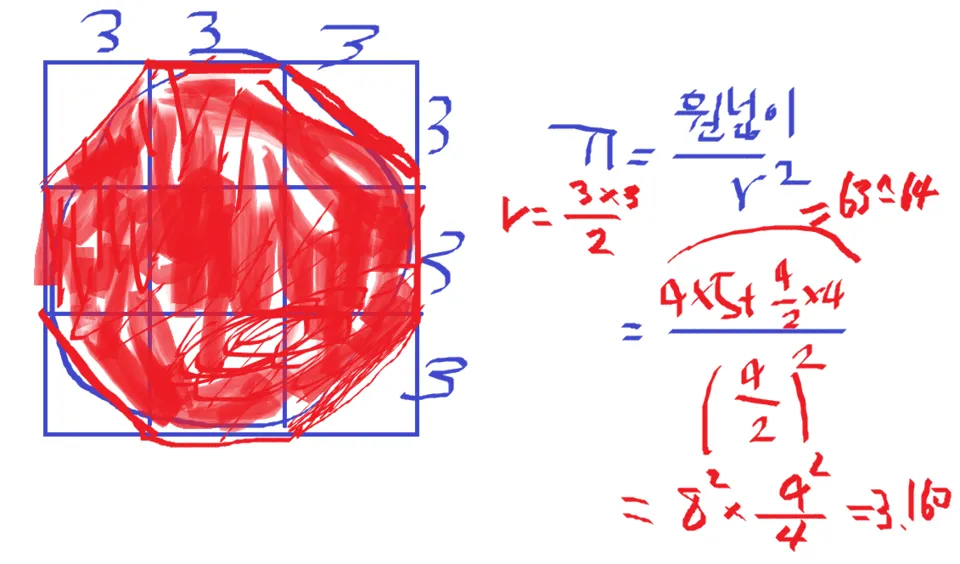
사실 Pi 의 근사값에 대해서는 유럽보다 아시아에서 더 먼저 정확히 계산을 했다. 중국인 수학자 유휘는 아르키메데스의 정96각형 보다 더 큰 정 192각형을 이용하여 Pi 를 계산하였고 후에 5세기 경에는 이보다 더 엄밀한 3.141592 자리까지 계산하였는데, 유럽에서는 16세기가 다 되어야 이 정도의 근사값을 구했다고 한다.
이 16세기 값이 아마 비에트의 방법을 말하는 것 같다. 비에트는 삼각함수를 도입하여 pi 를 계산했는데 사실 이는 크게 아르키메데스의 방법과 다르지 않다. 그의 방법론은 2^k n 각형의 넓이를 구하고 n 을 무한대로 보냈을 때 원 넓이가 나온다는 것으로 이를 구하기 위해 먼저 n각형과 2n 각형의 넓이 비를 구했다.
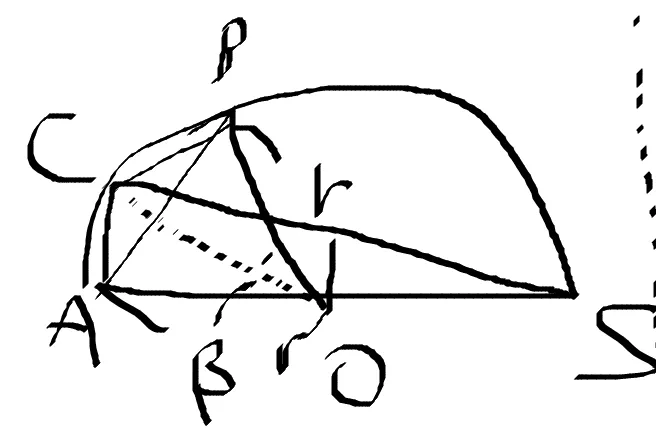
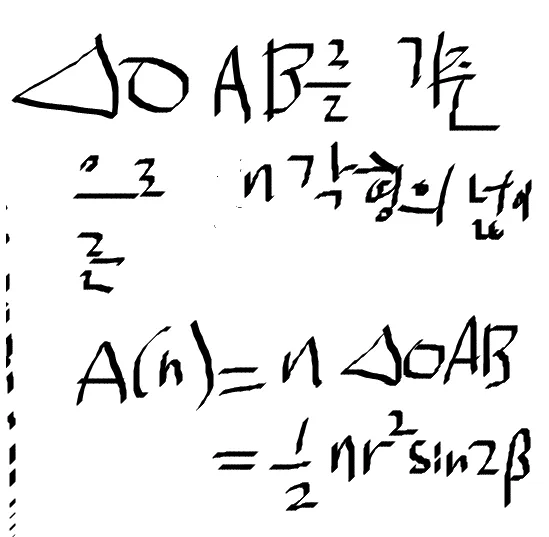
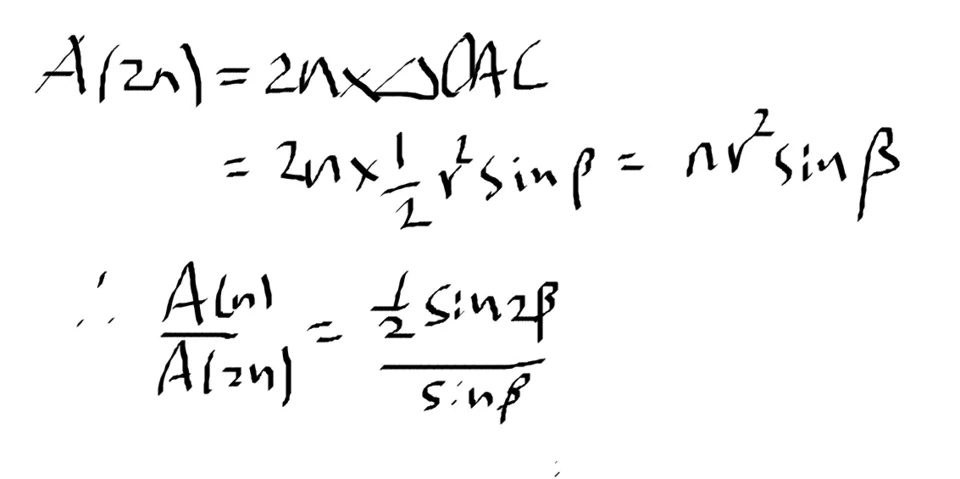
그리고 이를 반복하고 삼각함수 공식을 썼다. 결론적으로 그가 이용한 식은 다음과 같다.
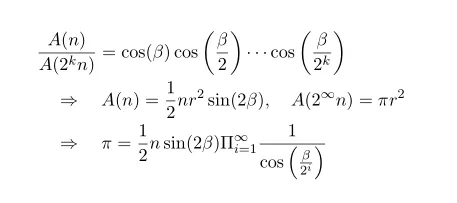
비에트 이후 유럽의 수학자들이 본격적으로 Pi 를 정확하게 계산하려고 시도하였으며 삼각함수, 특히 아크탄젠트 값을 정확하게 구하려는 시도를 통해 Pi 값을 구하기 시작했다. 16세기 말에는 30자리, 18세기 말에는 130자리까지 구했다고 한다. [미적분의 발달로 Pi 값의 정확도는 더 높아졌다 ]
참고로 그레고리-라이프니츠 급수, 뉴턴의 미분법을 이용한 (역삼각함수의 테일러 급수를 이용) Pi 계산법 등으로 pi 를 구할 수 있다. 후에 오일러는 이들을 응용해 arctan 값을 이용해 Pi 를 구하기도 했다. [오일러는 무한 급수를 정말 잘 다룬 학자이다. ]
이런 Pi 계산의 역사와 방법을 빠른 시간 내에 알고 싶다면 이 250장 짜리 책을 읽는 것을 추천한다. 무한급수를 이용한 다양한 Pi 방법들을 많이 소개하고 있지는 않지만, 중 고등학교의 수학 내용으로 충분히 따라가고 직접 계산해 볼만하게 설명하고 있어 읽는 것에는 크게 지장이 없을 것이라 생각한다.