전에 포스팅 했던 [수학, 책] 리만가설 를 보면 zeta 함수의 nontrivial zero 를 구하기 위해 zeta 함수 관련 reflection formula 를 사용하게 되죠
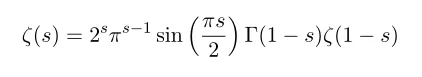
그 때 이 식의 유도 과정에 등장하는 항등식, Euler-reflection formula 에 대해서 알아보려고 합니다.
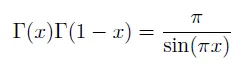
이 식의 가장 유명한 증명은 sin 함수를 곱으로 표현한 공식과 gamma 함수의 곱에 대한 표현식을 이용한 방법입니다. 저 리만가설 포스팅에도 소개했듯이 이 식을 증명하는데 크게 3가지 방법이 있습니다. 오늘은 그 중 첫번째 가장 대중적인 증명을 소개합니다. [1. Basel problem 을 이용한 풀이, 2. 복소함수 적분을 이용한 풀이 3. 미분방정식을 이용한 풀이 ]
먼저 감마함수와 sin 함수의 다른 표현식으로부터 시작합니다.
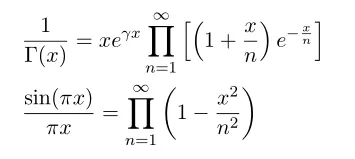
첫번째 식은 일종의 감마함수에 대한 정의이고 두번째 식은 Basel problem 으로 오일러가 구한 식입니다. 예전에 만든 노트가 있어 첨부합니다.

자 그럼 이제 reflection formula 로 돌아가 보죠. 그냥 드립다 공식 대입을 하면 바로 구할 수 있습니다. [그래서 가장 쉬운 풀이이죠]
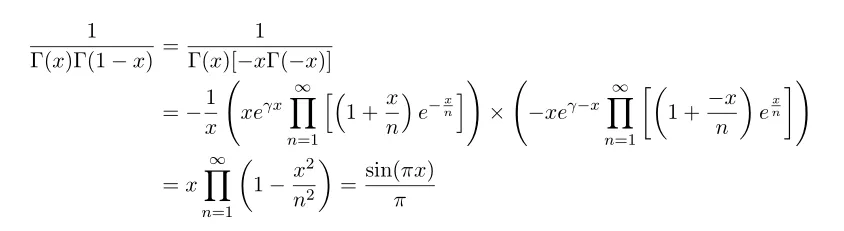
참 쉽지 않습니까? 문제는 이런 한가지 풀이를 가지고 만족할 제가 아니란 거죠.... 한번 일련의 여정(?) 을 통해 다른 풀이 방법을 소개해 볼까 합니다. 오늘은 그냥 맛보기만 하는걸로 ㅎㅎ