퀴즈 393 7개의 방과 10명의 손님
7개의 방이 있는 호텔에 10명의 손님이 찾아왔다. 이 10명 중 어떤 7명을 선택해도 그 사람들이 서로 다른 7개의 방에 들어갈 수 있도록 전체 10명의 사람들에게 열쇠를 나누어 주고 싶다.
이 때 열쇠는 최소 몇개가 필요할까?
풀이
28개, 사실 이 문제에서 28개가 나오는 것은 쉽게 구할 수 있는데, 문제는 이 28개가 최소임을 보이는 것이다. 하나씩 차분히 해보자.
먼저 방이 7개니까 7명에게 각 방 하나씩 열쇠를 주었다고 가정하자. 그리고 남은 3명을 생각해보자. 남은 3명을 어떻게 열쇠를 주어야 이 10명중 임의로 7명을 뽑았을 때 모든 방을 열 수 있을까?
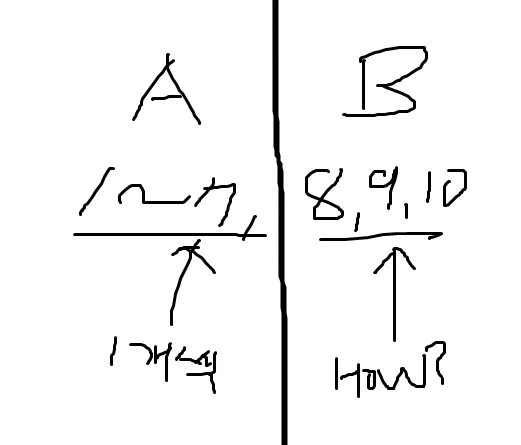
예를 들어 A에서 6명을 뽑고 B 에서 1명을 뽑았을 때 모든 방의 열쇠를 들어가게 하려면 B 에서 뽑은 그 한명은 7개의 열쇠를 가지고 있어야 한다. 이 3명을 뽑는 경우는 임의의 경우이니까 각각 7개씩 3개 총 B 그룹에는 21개의 열쇠가 들어가게 되고 전체 필요한 열쇠의 갯수는 7+21=28 개가 된다.
최소임을 보이라고 했으니 27개는 이 경우를 만족하지 않는다는 것을 보이면 된다. 자 7개의 방 중 하나를 선택 했을 때, 그 방(편의상 그 방을 x라 하자)의 열쇠를 가진 사람이 많아야 3명인 방이 존재한다. [열쇠의 갯수가 27개이고 이를 7로 나누면 몫이 3이다.] 즉 어떤 특정 방 x 의 열쇠를 가지고 있는 사람은 많아야 3명이다. 그럼 그 방 x 의 열쇠를 가지고 있지 않은 사람은 (10-3=7)명이 되는데 이 경우 이 7명을 뽑았을 때 x 방을 들어가지 못하므로 모순이 생긴다.
즉 27은 불가능하다.
일반화
이 문제를 일반화해보자
m 개의 방이 있고 n 명 (n>m) 의 손님이 있다. 이 때 n 명중 임의의 m 명을 선택해도 그 사람이 서로 다른 m 개의 방에 들어갈 수 있도록 n 명에게 열쇠를 주고 싶을 때 최대, 최소 몇개의 열쇠가 필요할까?
답은 최대는 mn, 최소는 m(n-m+1) 개가 될 것이다.