여분 차원의 글 에서 @rubymaker 님께서 차원에 대해서 한 코멘트로
플랫랜드편 시작합니다. 사실 이 책은 물리학과 수학을 사랑하는 사람들이 성경 처럼 가장 많이 읽은 책 중 하나이다! [하지만 원래는 사회적 계급에 대해 까는 풍자소설로 시작됬지만... 후폭풍은 과학에서!!!!]
주석이 없는 원본 번역 책
얘를 보거나 주석이 달린
주석 때문에 책이 두배가 되어 버렸지만(가격도 두배...)... 저자의 배경이나 숨겨진 의미들도 해석해 주어서.. 다만 스스로 생각하시는 분들은 주석 없는 것을 읽으시는게...
심지어 영화도 있다. [영어 자막이지만 ㅠㅠ]
어려운 영어가 안 나와서 충분히 볼만하다!!!
그리고 무엇보다 스토리가 흥미진진하다!!!
유투브 영화 링크를 걸어둔다
ㅋㅋㅋㅋ 1시간 반짜리 영화인데 ㅋㅋㅋ
글을 쓰다가 심심해서 틀었다가 두번이나 봤군...
근데 역시 볼때마다 재밌다. ㅋㅋㅋㅋ
[사각형이 영화의 주인공인 A square 이고 옆에 직선이 주인공의 부인이다. ]
영화 내용을 이야기하자면 강력한 스포가 될테니...
스토리가 궁금한 분들은 나무위키 의 스토리 부분을 참조하시길...
여기도 사람 사는 곳이라 각종 사건사고가 일어난다;; ㅋㅋㅋ
여담으로 책의 내용과 설정을 알고 영화를 보면 꿀잼이다. [영화는 책의 내용을 각색해서 만들었다. 겹치는 내용들도 많긴 한데 다른 부분들 빠지고 새로 추가된 부분들 등이 있다. 이 또한 영화를 보는 숨겨진 재미! - 슬프게도 영화와 책의 결말은 다르지만 길게보면 둘다 ...]
책과 영화의 플랫랜드는 경직된 계급사회인데[도형에 따라, 남녀에 따라.. 색깔에 따라....] 거기서 벌어지는 정치적 갈등과 이야기거리가 현실문제들을 상당히 반영, 풍자하고 있어서 ㅎㅎ
일단 2차원을 중심(플랫랜드)으로 이야기를 해보자.
2차원에서 사는 도형들은 어떻게 서로를 구분할까? [서로 말하는 것을 제외하자
나는 삼각형이야, 4각형이야, .... 재미없지 않는가.. 거기다 거짓말을 한다면...]
가장 쉬운 것은 서로 만져서 구분할 수 있겠다. 만지는 것으로 꼭지점 갯수와 선분의 길이를 파악 할 수 있을 테니까
만지지 말고 단순히 보는 것으로 서로서로를 어떻게 구별 할 수 있을까?
2차원(플랫랜드)에서는 서로서로를 선으로밖에 볼 수 없다.
가까이 다가간다면 선이 커 보일것이고 멀어진다면 선이 작아질 것이다.
일정 거리를 유지하고 360도를 돌면서 이 선의 길이의 변화와 주기성을 살펴보면
비교적 쉽게(?- 어렵다..) 구분할 수 있다.
반면 2차원 물체가 1차원 물체를 구분하는 것은 매우 쉽다.
[1차원 에게는 앞 뒤 밖에 없겠지만 2차원 에서는 앞, 뒤, 좌, 우 가 있을 테니...]
3차원 물체는 2차원에서 어떻게 구별할까?
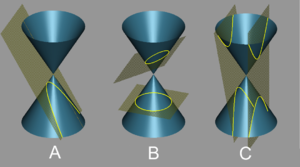
정사영을 통해서 형태를 볼 수 있다. 예를 들어 구 같은 경우는 수직으로 들어왔을 때 처음엔 점이었다가 점점 원이 커지고 다시 줄어들고 점으로 되는 것을 볼 수 있을 것이고 원뿔이나 원기둥 들도 2차원에 들어오는 각도에 따라 타원, 원, 쌍곡선 등의 모습을 볼 수 있을 것이다.
사실 이런 것들은 이미 고등학교 때, 이차곡선, 원뿔 곡선을 배우며 접한 내용이다.
여담 : 3차원의 것들은 어떻게 서로를 구분할까?
차원 이야기를 좀 더 해보자.
책과 영화속에 도형들은 각자 자기가 사는 space 에 대한 정의가 다 다르다.
1차원에 사는 사람에게 있어 space 는 length 밖에 없을 것이고
2차원에 사는 사람에게 있어 space 는 length, width 밖에 없을 것이고
3차원에 사는 사람에게 있어 space 는 length, width, height 밖에 없을 것이고..
이런 식으로.. (차원 별로 1차원의 길이에 해당되는 것들이 늘어난다. -척도가 늘어난다. )
각자 자기가 사는 세계의 frame 에 얽매여 있다.
고차원의 존재가 자기보다 낮은 차원의 세계에 찍접(?) 되는 것은 쉬우나 반대의 경우는 어렵다.
사실상 고차원의 존재가 그 모습을 드러내는 것 이외에는 우리는 우리가 살고 있는 계를 깨고 나오기가 매우 힘들다.
물론 이론상(수학적으로)으로 우리보다 더 높은 차원이 있고 우리는 그 차원에 embeded 되어 그 hypersurface 에 살고 있다고 말을 할수는 있겠지만....
영화와 책 속에서는 3차원의 구가 이상한 기계를 통하여 1차원의 선과 2차원의 사각형을 3차원의 세계로 대려온다!
그리고 3차원의 구 A sphere 가 2차원의 A square 과 1차원의 A line 에게 더 높은 차원(3차원)의 존재를 이해하지 못하냐고 꾸중하지만, A square 가 한 질문(3차원보다 더 높은 4차원의 존재)에 대해 이야기를 하면 화를 내는 그런 모습들이 나온다. [책 제목이 Flatland!! A square 는 정말 똑똑한 친구로 나온다!]
결국 자기가 같힌 프레임을 스스로 깨는것이 얼마나 어렵다는 것을 보여주는 또 다른 예가 될 수 있다...
흠.. 나도 똑같이 살아가고 있지는 않은가 반성을 해본다.
참고로 영화의 마지막 신이 우리에게 시사하는 부분이 굉장히 크다.
참고문헌
주석달린 플랫랜드